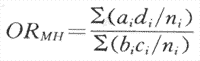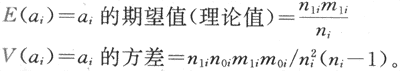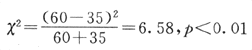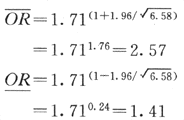流行病學/病例對照研究
| 醫學電子書 >> 《流行病學》 >> 流行病學分析性研究 >> 病例對照研究 |
| 流行病學 |
|
|
|
(一)概說
病例對照研究(casecontrol study)是主要用於探索病因的一種流行病學方法。它是以某人群內一組患有某種病的人(稱為病例)和同一人群內未患這種病但在與患病有關的某些已知因素方面和病例組相似的人(稱為對照)作為研究對象;調查他們過去對某個或某些可疑病因(即研究因子)的暴露有無和(或)暴露程度(劑量);通過對兩組暴露史的比較,推斷研究因子作為病因的可能性:如果病例組有暴露史者或嚴重暴露者的比例在統計學上顯著高於對照組,則可認為這種暴露與患病存在統計學聯繫,有可能是因果聯繫(圖4-1)。究竟是否是因果聯繫,須根據一些標準再加以衡量判斷(詳見第七章「病因及其推斷」)。所謂聯繫(associatiom)是指兩個或更多個變數間的一種依賴關係,可以是因果關係,也可以不是。
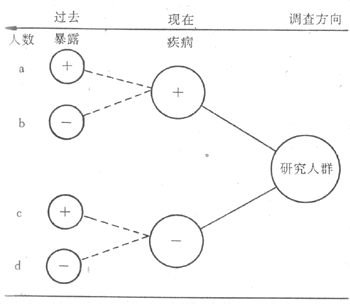
圖4-1 病例對照研究示意圖
例如,對一組肺癌病人(病例組)和一組未患肺癌但有可比性的人(對照組)調查他們的吸煙(暴露)歷史(可包括現在吸煙否,過去吸過煙否,開始吸煙年齡,吸煙年數,最近每天吸煙支數;如已戒煙則為戒煙前每日吸煙支數,已戒煙年數,等等)。其目的為通過比較兩組吸煙史的差別,檢驗吸煙(可疑病因)與疾病(肺癌)有因果聯繫的假設。這就是病例對照研究。
實例1.吸煙與肺癌的關係。
英國流行病學家A.B.Doll與R.Hill於1948~1952年進行過一項病例對照研究。他們從倫敦20所醫院及其他幾個地區選取確診的肺癌1465例。每一病例按性別、年齡組、種族、職業、社會階層等條件匹配一個對照;對照系胃癌、腸癌及其他非癌症住院病人,也是1465例。由調查員根據調查表詢問調查。經分析數據,得到的主要結果有:①肺癌病人中不吸煙者的比例遠小於對照組:男性佔0.3%,女性佔31.7%;而對照組中男性不吸煙者佔4.2%,女性佔53.3%,差別均很顯著;②肺癌病人在病前10年內大量吸煙者(≥25支/日)顯著多於對照組;③隨著每日吸煙量的增加,肺癌的預期死亡率。(推算出的年死亡率)也升高,例如男性45歲~64歲組日吸煙25~49支者與不吸煙者死亡率之比為2.94/0.14,即前者的率為後者的21倍;④肺癌病人與對照組比較,開始吸煙的年齡較早,持續的年數較多,而病例中已戒煙者的停吸年數也少於對照組中已戒煙者。
以後,Hill,Doll,Peto等又用前瞻性隊列研究法深入研究,經長達20年(女性經22年)的觀察,更加令人信服地提示出吸煙為肺癌的主要病因以及吸煙對健康的其他多種危害。他們的結論已為其他許多研究所證實,成為許多國家提倡不吸煙、限制吸煙及限制捲煙銷售政策的科學基礎。
病例對照研究是最常用的分析流行病學方法。因其需要的調查對象數目較少,人力、物力都較節省,獲得結果較快,並且可由臨床醫生在醫院內進行。對於少見病的病因研究,常為唯一可行的方法。但這些優點都是與前瞻性隊列研究相對而言的,實際上倘與同等規模的臨床研究或實驗室研究比較,病例對照研究所費的時間與精力可能更多。
本書以臨床醫學專業學生為主要讀者,並不要求他們能掌握或獨立應用分析流行病學方法,目標只是了解大概、擴大眼界、培養科學思辨能力,領會科學上獲得一個發現或作出一個結論的複雜過程及需要的客觀態度。
病例對照研究是從現在是否患有某種疾病出發,回溯過去可能的原因(暴露),在時間順序上是逆向的,即是從「果」推求「因」,所以又稱回顧性調查、研究。
病例對照研究(及其他類型的流行病學研究)中所謂的暴露(exposure)是指研究對象(病例或對照)具有某種疑為與患病與否可能有關的特徵或曾受到某種疑為與患病與否可能有關的因子的影響。所謂特徵(characteristic)可以是體質上的、生理上的、也可是心理精神上的;即可以是遺傳性的也可以是獲得性的;所謂因子(因素)既可以是外界的也可以是機體內在的;特徵或因子可以是致病性的,也可以是保護性的(使人免於患病的)。因此,「暴露」是一個涵義廣泛的概念。
(二)方法
1.樣本含量的估計 為了研究一種暴露與疾病的關係需要多大一個樣本,也就是需要多少個病例和多少個對照,首先取決於4個條件:①人群中暴露者的比例;②假定暴露造成的相對危險度(其涵義詳見後文);③要求的顯著性水平;④要求的把握度。從這4個條件估算樣本的含量的方法,詳見附錄五。實際上,樣本含量還受許多因素的制約,例如病例和對照的來源、財力、人力、完成期限等。假定只有一定數目的病例與對照可以利用,則一個研究能查出的最小相對危險度是多少?又假定經費數目已限定,則應選多少個病例與對照才能取得最大的把握度,這些都是應考慮的問題。此外,評價交互反應,控制混淆因素,亞組分析,每例多個對照等均影響所需樣本的大小。
2.病例和對照的來源與選擇
(1)病例:主要有兩種來源:①從醫院病人選擇,即是從某一所或若干所醫院選擇某時期內就診或住院的某種病的全部病例。病例應符合統一的、明確的診斷標準。最好是新發生的(新診斷的)病例。因為一種病的全部病例不大可能都有進入某一所或幾所醫院的同等機會,能進入的只是其中符合條件(即選擇因素)的那一部分,所以不要求能代表某時某地的全部病例,但應要求能代表產生病例的人群,即該人群只要發生該種病例均可能進入該院。這樣,結果的普遍性雖受限,但真實性不受影響,而真實性是普遍性的前提。這種研究稱為以醫院為基礎的(hospital-based)病例對照研究;②從某特定人群選擇病例,即是以符合某一明確規定的人群在某時期內(一年或幾年,視病例發生多少而定)的全部病例或當病例數過多時以其中的一個隨機樣本作為研究對象。其優點是選擇偏倚比前一種來源的小,結論推及該人群的可信程度較高。這種研究稱為以人群為基礎的(population-based)病例對照研究。
(2)對照:設立對照的目的在於估計如果疾病與暴露無聯繫,則病例組的暴露率可能為多少,也就是為比較提供一個基準。因此,對照與病例在一些主要方面必須具可比性。首先,對照必須從病例所來自的人群選擇,對照是有可能成為病例的人,換言之,每一病例在未發病前應該是合格的對照,而每一對照若發病都有可能成為病例組的成員。對照選擇是否恰當是病例對照研究成敗關鍵之一。
通常的做法是:如果病例組來自某一特定人群,則可以該人群的非病例(即未患該種疾病的人)的一個隨機樣本作對照;如果病例來自某所醫院,則可從同醫院同時就診或住院的其他病例中選擇對照。要求對照具有和病例一致的某些特徵,即對照與病例有可比性,例如性別、年齡、居住地等;同時要求對照沒有患和研究因子與研究疾病有關的其他疾病的可能。例如,研究吸煙與肺癌的關係時,不能以慢性支氣管炎病人為對照,因為吸煙同時是這兩種病的可能病因;研究胃癌的病因不能以「慢性胃炎」病人為對照,因為這兩種病在病因上有密切關係,前者可能是後者在病因鏈上的一環。上述要求的目的都是減少混淆偏倚。其他來源的對照如病例的鄰居、同事、親屬等。各種不同來源的對照要解決的問題不同,都各有其局限性。例如,鄰居對照可控制社會經濟地位的混淆作用,兄弟姊妹對照是考慮控制早期環境的影響和遺傳因素的混淆作用(極端要求為用同卵孿生),配偶對照是主要考慮成年期環境的影響。最常採用的方式是對照和病例都選自同一醫院,因為理論上他們都來自該醫院所服務的同一人群,而且對兩者都可在相同的環境中進行調查,也易於合作。但是由於不同病種的患者入院的機會不同,有可能使本來與某病無關的特徵在醫院病例中表現出虛假的聯繫(詳見第七章「病因及其推斷」)。為了減少這種偏倚發生的可能性,應該選取多種疾病而不是一種疾病的病人作對照。
3.病例與對照的配合 設置對照的作用在於平衡除了研究因子(暴露)以外的其他可能影響患病的因素,也就是說如果暴露與所研究的疾病不存在聯繫的話,病例的暴露比例(率)應該與對照的無顯著差別;如果發現顯著差別,既然對照與病例在其他有關方面都可比較,因此可以推斷患病與否可能是與暴露率的差別有聯繫。為使兩者具可比性,首先可以通過限制選擇病例與對照的範圍(例如年齡範圍、性別、種族等),使有關因子儘可能齊同。病例組與對照組的某些特徵不應存在顯著差別,即應該均衡。
另一個選擇對照的重要方法叫匹配(matching,曾譯「配比」),又稱匹配抽樣(matchedsampling),就是在安排病例與對照時,使兩者的某些特徵或變數相一致。具體做法有兩種:一種叫成組匹配或頻數匹配,即在選擇好一組病例之後,在選擇對照組時要求其某些特徵或變數的構成比例與病例組的一致(即在兩組的總體分布一致),例如性別、年齡構成一致,具體做法上類似分層抽樣。另一種做法叫個別匹配,就是以每一病例為單位,選擇少數幾個特徵或變數方面與病例一致的一個或幾個對照者組成一個計數單位或計數和分析單位。一個病例匹配一個對照的(即1:1匹配)一般稱為配對,也就是說由一個病例和一個對照組成對子(pair)為一個計數單位。
個別匹配,特別是1:1匹配,最常被採用。理論上,一個病例可以匹配多個對照,但研究證明病例與對照之比超過1:4時,統計效率不會明顯增加,但工作量卻增大。如果病例與對照來源都充足,調查費用又差不多,則以1:1匹配最合適;如果病例數有限而對照易得,則可採用一個病例匹配幾個對照的辦法以提高統計效率(例如實例2)。
在病例對照研究中採用匹配的目的,首先在於提高研究效率(study efficiency),表現為每一研究對象提供的信息量的增加。匹配後再按匹配的因素進行分層分析,可使每一個匹配層中都有一定數目的病例與對照,不至於因有的層只有病例有的層只有對照而無法對比,不能提供信息。其次,在於控制混淆因素的作用。所以匹配的特徵或變數必須是已知的混淆因子,至少也應有充分的理由這樣懷疑,否則不應匹配。
無論是否採用匹配設計,為控制混淆作用都須在分析階段用分層、標準化或多元分析,但匹配後再按匹配因素作分層分析可以提高分析的效率,也就是提高了控制混淆因素的效率。
但是匹配也要付出代價:匹配增加了尋找對照的速度,以同樣的低價也許可以得到更多不匹配的對照,從而擴大樣本含量。從這個意義上說,匹配又降低了研究效率。增加匹配項目又會導致可能作為對照者的減少,無法找到可匹配對照的病例只得被剔除;一個項目一經匹配不但使它與疾病的關係不能分析而且使它與其他研究因子的交互作用也不能充分分析。把不必要的項目列入匹配,企圖使病例與對照盡量一致,如果匹配的因素與暴露有聯繫,就可能人為地造成更多的病例與對照暴露史一致的對子,徒然丟失信息,增加工作難度的結果反而是降低了研究效率。這種情況稱為匹配過度(over-matching),應注意避免。
匹配的變數應一致到什麼程度,取決於變數的性質、實際可能與必要:離散變數(即屬性,無中間值的變數)可以完全匹配,連續變數(在一定範圍內可取任何值的變數)往往劃分為若干類或組,再按此匹配。例如按年齡分組、按血壓分組、按吸煙量分組匹配。分得太細,會增加工作難度,也不一定必要,例如年齡要求同歲;但分得太粗,例如年齡按10歲分組,又達不到控制混淆作用的目的。
當估計有許多可能的混淆因素需要控制時,倘僅靠分層則因層數太多不能保證每層均有病例與對照,所以採用匹配以保證有效的分層分析。其次,有的列名變數包含許多類別或內容複雜(例如職業、種族、居住地、籍貫、兄弟姊妹等),如是可能的混淆因子,應加匹配。否則單靠分層不能控制混淆作用。
匹配可保證對照與病例在某些重要方面的可比性。對於小樣本研究以及因為病例的某種構成(例如年齡、性別構成)特殊,隨機抽取的對照組很難與之平衡時,個別匹配最為有用。
一般除性別、年齡之外,對於其他因素是否列入匹配須持慎重態度,以防止匹配過頭及徒增費用和延長完成時間。
4.計劃和執行 病例對照研究在制訂計劃和執行時應注意以下問題:
(1)主要假設的說明是否清楚、簡明而且可以檢驗?
(2)疾病與暴露變數的定義清楚、明確否?
(3)是否擬探索劑量反應關係和多個危險因素的聯合作用?
(4)為解答問題所需之病例數和對照數能否得到?這樣大小的樣本能查出的最小相對危險度是多少?與估計的相差多少?[參考附錄五(四)節]。
(5)病例來源及抽樣技術明確否?病例數與對照數之比是多少?匹配否及匹配哪些變數?
(6)調查表(問卷)是否已包括打算測量的所有變數並能夠收集到需要的數據?其詳盡程度是否已足供分析之用?
(7)醫院記錄(病歷)及其他來源的信息、從體檢、實驗室檢查、病理切片等獲得的數據需表格記錄否?
(8)調查表經過試用否?其真實度與可靠度(重複性)經評估否?訪問時擬使用幫助回憶的實物、模型或圖片否?
(9)調查員、質控員、病歷摘錄員、編碼員的工作手冊已編好否?須專門培訓否?
(10)組織機構、人員、設備、經費落實否?
(11)協作單位有書面協議否?有關領導機關已批准否?將診斷根據(切片、標本、影像圖片等)送到主持單位複核安排妥當否?
(12)實驗室檢驗項目或用儀器檢測的項目所用儀器、方法、試劑是否符合標準?結果的真實度與可靠度經過考核否?
(13)經治醫院、醫生是否同意提供病例和對照?是否必須取得研究對象在了解情況後的書面同意?資料、數據怎樣保密?怎樣保存?
5.數據分析 須分析什麼項目,計算哪些統計量,用什麼統計學方法,用手工(計算器)還是計算機,如用後者怎樣建資料庫和用什麼軟體包,等等,都應包括在設計之中,手工計算時還應擬好相應表格。現在計算機及統計軟體包的應用漸趨普及,過去很難進行的一些複雜的統計檢驗現在很快就可完成並列印出結果還可繪出統計圖。但是,一些流行病學專家主張先用手工計算基本內容以熟悉數據,然後再由計算機作複雜運算(多元分析)。
本節要介紹的是基本原理和基本方法,無論用手工或機器運算,這些都是應熟悉的。
病例對照研究數據分析的中心內容是比較病例和對照中暴露的比例並由此估計暴露與疾病的聯繫程度,並估計差別與聯繫由隨機誤差造成的可能性有多大,特別要排除由於混淆變數未被控制而造成虛假聯繫或差異的可能。進一步,還可計算暴露與疾病的劑量反應關係,各因子的交互作用(對一種因子的暴露會不會影響對另一種因子的效應),等等。非匹配和匹配設計的研究,數據的分析方法有一些不同。
(1)非匹配數據的分析:首先要檢驗病例組與對照組在某些主要特徵(即可能成為混淆因子的特徵)的構成上是否沒有顯著差別(均衡性檢驗)。
1)聯繫的顯著性與聯繫強度:某個因素與某種結局(患病或死亡)之間的聯繫是否有統計學顯著性,常用χ2檢驗。最簡單的情況是因素與結局都只分為「有」或「無」兩類,數據可納入一張2×2表(即四格表,又稱四格列聯表),例如表4-1。χ2檢驗可用四格表專用公式(式4-1)。但χ2值的大小並不表示聯繫的強度。χ2≥3.84時,設兩者無聯繫的假設(無效價設,H0)被否定,而轉向存在聯繫的假設(備擇假設,HA),這個判斷錯誤的可能性為≤0.05(即ρ≤0.05)。χ2值越大,判斷錯誤的可能性越小。
表4-1 危險因子與疾病的聯繫
| 患病 | 有暴露史 | 無暴露史 | 合計 |
| 有 | a | b | a+b |
| 無 | c | d | c+d |
| 合計 | a+c | b+d | a+b+c+d=n |
統計學顯著性可以評價在多大程度上可用機會解釋所觀察到的聯繫。但如數據本身存在系統誤差,統計學顯著性檢驗就無意義,因為它不能區別聯繫的真或假(由偏倚、混淆所致的聯繫)。此外,統計學顯著性檢驗結果極大地受樣本含量的影響,樣本小則隨機變異大;即使實際上暴露的作用很大,也會導致「不顯著」的結論。所以「不顯著」應理解為「不足以否定無效假設」。
現況調查和隊列研究(見本章「二、隊列研究」)可以計算暴露者(或具某特徵者)和未暴露者(或不具某特徵者)的患病率或發病率,因為分子數與分母數是已知的。也可以計算相對危險度(見本章公式4-11)。這是聯繫強度的一個指標。
但是病例對照研究因為不能計算出患病率或發病率所以不能計算相對危險度,但可用另一個聯繫強度指標——比數比(odds ratio,又譯比,值比、優勢比,縮寫為OR)。比數比是兩個比數之比。比數(odds)是表示一個事件發生機會大小的一種指標。以表4-1為例(字母代表數目),如果是隊列研究與現況調查,可以計算髮病(或患病)比數,暴露組的這個比數為α/c,未暴露組的這個比數為b/d。如果是病例對照研究,可以計算暴露比數,在病例組是α/b,在對照組是c/d。兩組比數之比稱為比數比,
OR =(α/b)/(c/d)=αd/bc
或
OR =(α/c)/(b/d)= αd/bc.(式4-2)
這個比正好是四格表中兩條對角線上四個數字的交叉乘積αd與bc之比,所以四格表數據的OR又稱交叉乘積比。OR可用於隊列研究,但更重要的是用於病例對照研究。在少見病,OR可以當作RR去解釋,即OR近似於RR。因在此情況下總體內不論暴露組或未暴露組中患病者的人數(分別記為A與B,用大寫字母區別於樣本數據的小寫字母)都遠少於未患病者的人數(C與D),所以在總體內A+C→C,B+D→D,於是
因為從隨機樣本的α/c與b/d可以估計A/C或B/D,所以可用αd/bc估計AD/BC,也就是說可以用OR作為RR的估計值。
暴露組與未暴露組的發病率或死亡率之比稱為率比(rate ratio)。兩組發病機率之比稱為危險度比(risk ratio)。在少見病,這兩個比和比數比均近似,可統稱為相對危險度。
從OR(或RR)值可估計暴露與疾病的聯繫程度。這種聯繫的穩定性,即隨機變異的大小可用顯著性檢驗的ρ值和可信限來估計。OR是用來估評暴露與疾病的聯繫程度或即暴露作用強度的一個點估計值(0~∞),但為估計這個值受隨機變異影響的程度,最好同時算出可能包括真值(參數)的一個取值範圍,表示以一定程度的信心估計參數值所在的範圍,稱為可信限或可信區間(confidence interval)。計算方法詳見附錄五。如果可信限包括了無效值(OR=1),說明該聯繫無顯著性;可信限的寬度又反映點估計值(OR)的穩定性,範圍寬說明估計值不穩定,也就是隨機變異程度大。所以現在認為僅計算出點估計值的意義有限,應同時計算出其可信限。
2)分層數據分析:病例對照研究在設計階段可採用的控制混淆因素的方法有限制與匹配。限制是指對採用研究對象的範圍加以限制,如混淆因素為列名變數(離散變數)可限定只採用某一類或幾類對象(例如性別、職業、地區等),如為連續變數可限定只採用某一範圍內(例如年齡組、段)的對象。其目的都是得到比較勻質的研究對象。如果一個因素在各對象間無差別或差別很小,它就不可能起到混淆作用,也就是得到了控制。可在分析階段採用的控制混淆因素的方法有分層、標準化和多元分析。其中以分層分析最常用。
分層就是把樣本按照一個或更多個混淆因子的暴露有無或作用程度而劃分為若干個組,也就是「層」,再分別在每一層內分析所研究暴露與疾病的聯繫,計算各層的比數比(記為OR);
表4-2 第i層內病例與對照按暴露有無分組
| 組別 | 病倒 | 對照 | 合計 |
| 暴露 | αi | bi | m1i |
| 未暴露 | ci | di | m0i |
| 合計 | n1i | n0i | ni |
如果各層 具有齊性[齊性檢驗方法見附錄五(一)],則可以計算總的即各層OR的合併OR。因其方法系Mantel與Haenszel兩人所開發,所以通常記作ORMH。因在同一層內作為分層標誌的因子對病例組與對照組的作用都是相同的,所以對所研究的暴露與疾病的聯繫便不會發生混淆作用。其原理與匹配相同,實際上1:1匹配就是一種最細的分層,每層只包括一個病例與一個對照。合併OR是概括各層OR的一個指標。
合併OR的計算方法:
ORMH可信限的計算方法及計算實例見附錄五(一)。
ORMH如果不等於1,那麼與1的差異是否顯著?可用作顯著性檢驗,其方法如下:
式中,ai=各層四格表中的a數值,
檢驗假設(即無效假設)Ho:OR=1,雙側備擇假設HA:OR≠1。統計量X2MH呈自由度為1的X2分布。
分層分析法舉例:某地進行了一次食管癌病因的病例對照研究,共調查病例200例,人群對照776例。現分析其中飲酒與食管癌的聯繫,結果如表4-3。
表4-3 飲酒與食管癌的聯繫
| 飲酒史 | 病倒數 | 對照數 | 合計 |
| 飲 酒 | 171 | 381 | 552 |
| 不飲酒 | 29 | 395 | 424 |
| 合計 | 200 | 776 | 976 |
OR=6.11 χ2=84.29
可見飲酒與食管癌有強聯繫,但已知吸煙與食管癌也有強聯繫。為了分析飲酒與食管癌顯示出的強聯繫是否可能與吸煙有關,或吸煙是否可能是一個混淆因子,可採用分層分析:按是否吸煙分為兩組,再分析飲酒與食管癌的聯繫,結果見表4-4。
表4-4 飲酒與食管癌在吸煙與不吸煙者的聯繫
| 不吸煙者 | 吸煙者 | ||||||
| 飲酒史 | 病倒 | 對照 | 合計 | 飲酒史 | 病倒 | 對照 | 合計 |
| 飲 酒 | 69 | 191 | 260 | 飲酒 | 102 | 190 | 292 |
| 不飲酒 | 9 | 257 | 266 | 不飲酒 | 20 | 138 | 158 |
| 合計 | 78 | 448 | 526 | 合計 | 122 | 328 | 450 |
OR=10.3 χ2=53.99 OR=3.70 χ2=24.62
計算ORMH,先用公式(4-3)計算
再用公式(4-4)作χ2檢驗:
χ2MH=76.84
ρ<0.00000001。用附錄五公式(附式5-1)計算ORMH的95%可信限,上限為8.09,下限為3.81。用附錄五(一)的Woolf法作各層ORi的齊性檢驗,結果說明各層間的OR差異顯著,來自同一總體的可能性很小,所以ORMH不能說明吸煙、飲酒與食管癌的聯繫,因此是無意義的。這種齊性檢驗可同時檢驗各因素間是否存在交互作用。本例的計算過程及結果解釋見附錄五(一)的計算實例。
以上關於分析方法的介紹,都是以暴露有無和疾病有無這種最簡單的兩分變數為例。實際情況常較此複雜,有必要時讀者可參考專書。
多個混淆因子如用分層法同時控制多個混淆因子,則分成的層數將很多(例如,年齡分組,性別分組,吸煙與否2組,就已有20層),在樣本含量不是特別大的情況下,每層的人數將劇減,而且各層中病例數與對照數或與未暴露者數目的比例波動很大,可能出現只有病例而無對照或相反以及人數為零的層,以致統計效率降低,信息丟失。這時應採用多元分析法解決問題。現在藉助電子計算機及軟體包,已可使過去用手工計算很難進行的幾種方法成為普及。多元分析法在樣本不是極大的情況下可同時控制多個變數的作用而不影響研究效率。現在應用十分廣泛的是多元logistic回歸分析。
(2)匹配數據的分析:本書只以1:1匹配的數據為例。數據分析的程序基本上與非匹配數據相同。
1)檢驗病例與對照的暴露比例是否有顯著差別:就每一對中的病例與對照的暴露史而言,可能有四種組合情況(頻數記為f ,有暴露記為下標1,無暴露記為下標0):①病例有暴露,對照也有暴露(記為f11);②病例有暴露,對照無暴露(f10);③病例無暴露,對照有暴露(f01);④病例與對照都無暴露(f00)。只有這四種組合,而且四者必居其一。設四種情況的對子各有f11,f10,f01,f00對,則全部數據可用一張四格表歸納(表4-5)。每格的數字代表對子數。
設暴露與患病無聯繫,即H0:OR=1,x2檢驗用下式:
表4-5 配對數據的四格表
| 病倒 | 對照 | 合計 | |
| 暴露 | 未暴露 | ||
| 暴 露 | f11 | f10 | f11+f10 |
| 未暴露 | f01 | f00 | f01+f00 |
| 合計 | f11+f01 | f10+f00 | N |
自由度=1。此式適用於較大樣本。
2)比數比及其可信限的計算:只有病例與對照暴露史不相同的對子(f10與f01),才能提供關於暴露與疾病聯繫程度的信息。
OR=f10/f01(f01≠0時)(式4-6)
OR可信限可用附錄五公式(附式5-1)計算。
實倒1:有一項調查心肌梗死與高血壓的關係的病例對照研究,用1:1匹配設計,以收縮壓(SBP)≥18.6kPa(140mmHg)為高血壓。數據如表4-6(虛構)。
表4-6 高血壓與心肌梗死的病例對照研究
| 心肌梗死病倒 | 對 照 | 合計 | |
| SBP≥18.6 | SBP<18.6 | ||
| SBP≥18.6 | 15 | 60 | 75 |
| SBP<18.6 | 35 | 40 | 75 |
| 合計 | 50 | 100 | 150 |
用公式(式4-5)作卡方檢驗:
用公式(式4-6)計算OR:
OR=60/35=1.71
用附錄五公式(附式5-1)計算OR的95%可信限:
計算結果說明高血壓與心肌梗死有中等程度的聯繫(OR=1.71)。高血壓患者患心肌梗死的危險度較非高血壓者約高出70%。OR的可信限不包括1,說明OR值有顯著性。
(3)人群歸因危險度:在一定條件下,從病例對照研究結果可以算出人群歸因危險度,詳見「隊列研究」。
(三)病例對照研究的偏倚
偏倚問題將在第七章詳細討論。三種主要偏倚,即選擇偏倚、信息偏倚、混淆偏倚,在病例對照研究都可能發生。特別是選擇偏倚,在醫院為基礎的病例對照研究更易發生。又因作為一種回顧性調查,特別易受回憶偏倚(信息偏倚的一種)的影響,因為暴露史主要須依靠被調者的回憶,但一些複雜煩鎖的問題(如膳食史)很難正確回憶;一些被認為可能與患病有關的暴露史,病例易高估,對照易低估。如果調查員知道誰是病例誰是對照以及病因假設,則易於在調查時態度不同、重點不同,產生誘導作用,從而造成偏倚,稱為調查員偏倚。這些都是在設計、執行和分析時應加預防和處理的。
實例2:女青年陰道腺癌(vaginal adenocarcinoma)和母親妊娠期服用已烯雌酚關係的研究。美國波士頓婦產科醫生AL Herbst注意到1966~1969年期間在該市Vincent紀念醫院診斷了7例~22歲的女青年患陰道腺癌。這本是一種罕見的女性生殖系統癌症,發病年齡一般在50歲以上。現在這種明顯的時間和地區的聚集性以及大為提早的發病年齡,引起了Herbst醫生探究其病因的興趣。
初步調查結果發現這7例均無使用陰道局部刺激物的歷史,除1例於發病後結婚外均否認有性交史。為詳細了解這些病例從胚胎期至發病前的情況以及她們的母親在妊娠期的情況,從而尋找病因線索,Herbst決定作一次病例對照研究。
另外,同時期在另一所醫院也診斷了一例20歲的陰道腺癌病人。這樣,共有8個病例。每例匹配4個對照。從病例出生的醫院保存的出生記錄中選擇與病例在同等級病房中前後不超過5天出生的女嬰作為對照候選人,優先選擇與病例出生時間最近者為對照。由經過訓練的調查員用調查表對病例、對照以及他們的母親進行訪問調查。
在列入比較的許多因素中,多數在兩組間無顯著差別。例如,出生時母親的年齡、母親吸煙史、哺乳史及X線照射史等。但有3個因素顯示顯著差別:母親以前流產史,此次懷孕時陰道出血史,此次妊娠期曾用過已烯雌粉(DES)。三者的關係是:因有前兩個因素存在才用DES治療。尤以DES服用史差別最為明顯(x2=23.22,p<0.00001)。
通過8個病例與32個對照的病例對照研究,Herbst等得出結論,母親在妊娠早期服用DES可使其在子宮內受暴露的女兒以後發生陰道腺癌的危險性增加。
實際上,在妊娠期用過DES的婦女很多,但她們的女兒發生陰道腺癌的危險並不高。病例對照研究結果提供的不是暴露招致的絕對危險度(發病率)而只是相對危險度。
從方法選擇上,DES與陰道腺癌的聯繫問題,還可用歷史性隊列方法研究:收集在病例診斷前15~25年間曾在妊娠期用過DES的婦女的住院病歷,再選擇合適的、未用過DES的婦女的病歷作為對照組。對兩組婦女的女兒們進行隨訪,確定陰道腺癌的發生率是否有差別。因為這是一種罕見病,這樣研究雖然理論上可行,但實際做起來困難很多。至於用前瞻性隊列法研究罕見病的病因,雖然理論上也可行,但實際上做不到。因此,可以看出:病例對照法是研究罕見病的最經濟最快捷的途徑,常常是唯一實際可行的途徑。Herbst等只用8個病例與32個對照所完成的病例對照研究就是一個有意義的例子。
參看
| 關於「流行病學/病例對照研究」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |