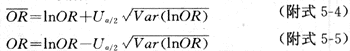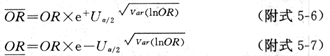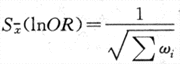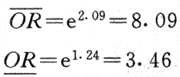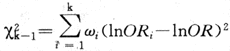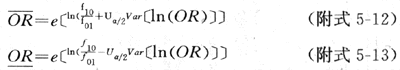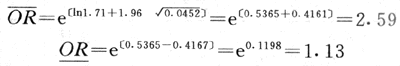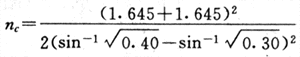流行病學/分析流行病學有關計算

醫學電子書 >> 《流行病學》 >> 分析有關計算

流行病學

流行病學緒論 疾病的分布 流行病學描述性研究 流行病學分析性研究 診斷試驗及疾病篩檢的評價 臨床療效和預後分析 病因及其推斷 傳染病流行病學 疾病的預防措施 醫院感染 各種傳染病的潛伏期和病人及接觸者的管理方法 消毒 殺蟲 滅鼠 分析流行病學有關計算 確定診斷標準 率的調整或標準化 進一步學習用參考書目錄

流行病學目錄

（一）OR、OR_MH的可信限和OR_i的齊性檢驗

⒈Miettinen法　即是以顯著性檢驗為基礎的（test-based）可信限。計算OR_MH的100（1-α）％可信限公式

此公式同樣可用於計算單個OR（即從一張四格表數據算出的OR）的可信限。這時，上式中用OR代替ORMH，用x²代替X²_Mh。匹配數據的OR也可同樣計算。用函數型電子計算器來算，都很簡單。

式中的U，可查標準正態差簡表（附表5-1），U_α/2可查α/2單側檢驗的U_α值。最常用的95％可信限按下式計算（上限記為OR_U，或OR，下限記為OR_L或OR）:

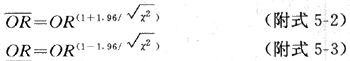
附錄5-1　標準正態差簡表

α（或β）	單側檢驗時Uα(或Uβ*)	雙側檢驗時Uα
0.001	3.09	3.29
0.005	2.58	2.81
0.010	2.33	2.58
0.025	1.96	2.24
0.05	1.64	1.96
0.10	1.28	1.64
0.20	0.84	1.28
0.30	0.52	1.04

* 双侧检验时U_β值與單側檢驗時相同

計算實例：表4-4的數據，OR_MH＝5.55，x²_MH＝76.84，95％可信限：

2. Woolf法　即自然對數轉換法

（1)首先把OR轉移為自然對數，記為lnOR；

(2)按下式求出lnOR的方差，記為Vαr(lnOR)：

即四格表中每一格數值的倒數之和。倘有某一格的數值為0時，可在每格的數值上各加0.5，再求出它們的倒數之和。

⑶lnOR的100(1-α)％可信限為

如為求95％可信限，上面兩式中U_α/2＝1.96；

(4)最後各取其反對數（e^X），即為OR的可信限。

(5)也可直接用下式算可信限：

以上都是用於計算不分層OR（粗OR）的公式，如為分層的數據也可用Woolf法計算各層lnOR_i的加權平均數及其可信限；同時可檢驗各層OR_i是否有齊性，即是否沒有顯著差異，倘有齊性，計算總的OR才有意義。

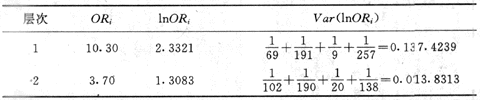
計算實例：仍用表4-4的數據，用公式（附式5-4）與（附式5-5）分別算出吸煙者與不吸煙者兩層中飲酒與食管癌的OR及其對數（lnOR）以及lnOR的方差和方差的倒數（w_i權重），結果列表如下：

總的OR用下式計算：

將上表數據代入：

結果與OR_MH(5.55)相當接近。再按下式求OR的標準誤：

（附式5-9）

得S_x(lnOR)=0.2169,於是lnOR的95％可信限lnOR±1.96S_x,代入得2.09，1.24，於是

與OR_MH的95％可信限（8.09,3.81）也十分接近。

但是各層的OR_i相關懸殊，或即吸煙者與不吸煙者中飲酒與食管癌聯繫強度差異較大，這種差異是隨機變異的機會有多大？可以用下式作x²檢驗：

（附式5-10）

式中k＝層數，自由度＝k－1。

代入本例數據，x²＝5.06，5.06>x²(1，0.025)，p<0.025，各層間的OR差異顯著，來自同一總體的可能性很小，所以總的OR不能說明吸煙、飲酒與食管癌的聯繫，因此是無意義的。

上述x²檢驗同時可用來檢驗各因素間是否存在交互作用。本例的結果提示吸煙與飲食這兩個因子與食管癌危險度的聯繫有交互作用。

以上兩種方法算得的都是似可信限，但在OR靠近無效值⑴的情況下，特別是在樣本較大時，近似法與精確法所得結果十分接近。

⒊ 匹配數據的OR可信限

可用Miettinen法〔以顯著性檢驗為基礎的方法，公式（附式5-1）〕，實例見第四章表4-11的數據分析。還可用下述方法：

(1)先算方差：

(2)OR 的（1－α）％可信限

計算實例：仍用表4-11的數據，計算OR的95％可信限。U_α/2＝1.96，OR＝1.71，Var(lnOR)＝(60＋35)/(60×35)＝0.0452，

結果與用公式（附式5-1）算得的（1.14，2.57）很接近，而且理論上更恰當。

（二）病例對照研究樣本含量的估計

所謂樣本含量估計是指在滿足一定條件下的一個粗略估計數；條件變動時估計數會隨之發生變化，所以只有相對意義，而不能看作是保證可達到目的的準確數值。

樣本含量（n）的估計須根據①對照人群的預防暴露率，p0；②暴露與疾病的聯繫程度，以RR為指標；③假陽性率，即Ⅰ型誤差，α；④假陽性率，即Ⅱ型誤差，β。

1.非匹配設計病例數與對照數相等時每組所需人數

式中P₁＝P₀RR/［1＋P₀(RR－1)］，p＝0.5(P₁＋P₀)，q＝1－P₀。U_α與U_β可查附表5-1。有時也可不用公式，通過查表即可得n，例如附表5-2。

附表5-2　病例對照研究樣本含量（非匹配，病例組與

對照組人數相等時每組需要人數）

α＝0.05（雙側），β＝0.10
RR	p0
	0.01	0.05		0.1	0.2		0.4	0.5		0.6	0.8	0.9
0.1	1420	279		137	66		31	24		20	18	23
0.5	6323		1286	658		347	203	182	176		229	378
2.0	3206		689	378		229	176	182	203		347	658
3.0	1074		236	133		85	71	77	89		163	319
4.0	599		134	77		51	46	51	61		117	232
5.0	406		92	54		37	35	40	48		96	194
10.0	150		36	23		18	20	24	31		66	137
20.0	56		18	12		11	14	18	24		54	115

(節錄：Schlesselman,1982)

例：現擬進行一項病例對照調查，研究吸煙與肺癌的關係。預期吸煙者的相對危險度為10.0，人群吸煙率約0.4。設定α＝0.05（雙側檢驗），β＝0.10，查表可見至少需病例與對照各20。樣本較小是因RR很大。如用公式（附式5-14）計算，得數也相近，（n≈22），稍有出入是計算時保留小數位數不同所致。

在α＝0.05（雙側檢驗）時，U_{a＝1.96，β＝0.10，Uβ＝1.28，於是式（附式5-14）可簡化為}

2. 非匹配設計病例數與對照數不等時

設：病例數：對照數1:c，則需要的病例數

式中，

，P1的計算同公式（附5-14）

對照數＝cn。

3.　1:1匹配（配對）設計　須加估計的不是總例數而是病例與對照暴露情況不同的對子數（即表4-10中的f10與f01），設為m，則

式中PRR/(1＋RR)。

需要的總對數（f11＋f10＋f01＋f00）設為M，則

式中p1＝p0RR/﹝1＋p0(RR-1)﹞，q1＝1-p1，q0＝1-p0

例：設對照暴露率p0＝0.3，α＝0.05，β＝0.1，為檢出RR＝2需要的

m＝［1.96/2＋1.28

186，即共需f10＋f01＝90對，總對數＝186。

（三）隊列研究與實驗性研究樣本含量估計

實驗性研究與隊列研究有許多共同之處，所以對其樣本含量的估計一併介紹。

1.隊列研究樣本含量　這裡只有計數資料的樣本含量估計。應用公式計算時，必須對暴露（在實驗性研究為處理）預期造成的與對照組的差別有一個估計數（下式中p0為未暴露組的事件發生比例；p1為暴露組的事件發生比例），這個估計數來自經驗或理論，並規定Ⅰ型或Ⅱ型誤差的機率（α與β）。

此為公式（附式5-14）的原式，（附式5-14）是其簡化式，符號的意義兩式相同。實驗性研究有時樣本較小，應用本式時要求事件發生比例兩組均≥0.2，≤0.8。

2.實驗性研究　除公式（附式5-18）外，還可用率的反正弦轉換法，適用於事件發生率在0.05～0.95之間，單側檢驗。如作雙側檢驗，可用α/2代替式中的α。

(1)實驗組人數（nt）與對照組的人數（nc）相等。

nt＝nc，

式中pc＝對照組假定的事件發生率

pt＝試驗組假定的事件發生率。

Uα，Uβ值查附表5-1。

(2)實驗組與對照組人數不等（nt/nc≠1設為λ）

nt＝λnc，N＝nt＋nc。有1個以上實驗組時（設為Υ組），N＝Υnt＋nc。

上面兩式中率的平方根的反正弦（sin-1或arcsin）是用弦度來表示的，可用函數型計算器的RAD方式直接計算，十分便。

計算實例　設計條件為實驗組與對照組各一，以死亡為測定的結局，隨訪期5年，單側備擇假設，pc＝0.40（對照組5年死亡率），pc－pt＝0.10，α＝0.05，β=0.05，λ＝1。代入式（附式5-19）：

nc＝491，nt＝491。N（兩組人數）＝nc＋nt＝982。

但實際工作中還應考慮失訪、退出、不依從等因素所造成的樣本量減少，在估計時應給予適當補償：設損失率為d，可用係數1/(1－d)乘nc，仍用上例，設d＝20％，則nc＝(1/0.8)×491＝614，nt＝614，N＝1228。

此例如用公式（附式5-18）計算，得nc＝490，設損失率（d）＝20％，則nc＝(1/0.8)×491＝613，nt＝613，N＝1226。可見兩法所得基本一致，而以反正弦轉換法更為簡便。

（四）從已知樣本含量估計能查出的最大相對危險度

一種常見的情況是樣本含量限於條件已經限定，研究者想估計一下這個樣本能夠以一定的把握度查出的相對危險度最大是多少（如為保護因素則為最小的相對危險度），如果與預計的相關較大，則應待樣本擴大後再進行分析，以免徒勞。

可用下式估計，式中n為每組例數，p0，α，β的意義均與公式（附式5-14）相同：

式中

A＝(Uα＋Uβ)2

B＝1＋2p0

C＝2p0﹝n(1－p0)－Ap0﹞

滅鼠 | 確定診斷標準

關於「流行病學/分析流行病學有關計算」的留言：	訂閱討論RSS
目前暫無留言
添加留言

更多醫學百科條目