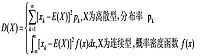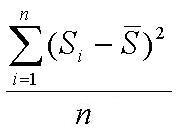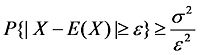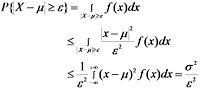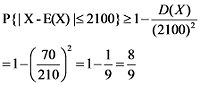方差
| A+醫學百科 >> 方差 |
在機率論和數理統計中,方差(英文Variance)用來度量隨機變數和其數學期望(即均值)之間的偏離程度。在許多實際問題中,研究隨機變數和均值之間的偏離程度有著很重要的意義。如下面的例子:
已知某零件的真實長度為a,現用甲、乙兩台儀器各測量10次,將測量結果X用坐標上的點表示如圖:
甲儀器測量結果:
乙儀器測量結果:
兩台儀器的測量結果的均值都是 a 。但是用上述結果評價一下兩台儀器的優劣,很明顯,我們會認為乙儀器的性能更好,因為乙儀器的測量結果集中在均值附近。
由此可見,研究隨機變數與其均值的偏離程度是十分必要的.那麼,用怎樣的量去度量這個偏離程度呢?容易看到E(|X-E(X)|)能度量隨機變數與其均值E(X)的偏離程度. 但由於上式帶有絕對值,運算不方便,通常用量
E{[X-E(X)]^2} 這一數字特徵就是方差。
目錄 |
方差的定義
設X是一個隨機變數,若E{[X-E(X)]^2}存在,則稱E{[X-E(X)]^2}為X的方差,記為D(X)或DX。
即D(X)=E{[X-E(X)]^2},而σ(X)=D(X)^0.5(與X有相同的量綱)稱為標準差或均方差。即用來衡量一組數據的離散程度的統計量。
方差刻畫了隨機變數的取值對於其數學期望的離散程度。
若X的取值比較集中,則方差D(X)較小;
若X的取值比較分散,則方差D(X)較大。
因此,D(X)是刻畫X取值分散程度的一個量,它是衡量X取值分散程度的一個尺度。
方差的計算
由定義知,方差是隨機變數 X 的函數
g(X)=[X-E(X)]^2
的數學期望。即:
由方差的定義可以得到以下常用計算公式:
D(X)=E(X^2)-[E(X)]^2
證明:
D(X)=E[X-E(X)]^2
=E{X^2-2XE(X)+[E(X)]^2}
=E(X^2)-2[E(X)]^2+[E(X)]^2
=E(X^2)-[E(X)]^2
方差其實就是標準差的平方。
方差的幾個重要性質
(1)設c是常數,則D(c)=0。
(2)設X是隨機變數,c是常數,則有D(cX)=(c^2)D(X)。
(3)設 X 與 Y 是兩個隨機變數,則
D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
特別的,當X,Y是兩個相互獨立的隨機變數,上式中右邊第三項為0(常見協方差),
則D(X+Y)=D(X)+D(Y)。此性質可以推廣到有限多個相互獨立的隨機變數之和的情況.
(4)D(X)=0的充分必要條件是X以機率為1取常數值c,即P{X=c}=1,其中E(X)=c。
常見隨機變數的期望和方差
設隨機變數X。
X服從(0—1)分布,則E(X)=p D(X)=p(1-p)
X服從泊松分布,即X~ π(λ),則 E(X)= λ,D(X)= λ
X服從均勻分布,即X~U(a,b),則E(X)=(a+b)/2, D(X)=(b-a)^2/12
X服從指數分布,即X~e(θ), E(X)= θ,D(X)= θ^2
X服從二項分布,即X~B(n,p),則E(x)=np, D(X)=np(1-p)
X 服從常態分佈,即X~N(µ,σ2), 則E(x)=µ, D(X)=σ^2
若Xi~ N(µi,σi^2),i=1,2,…n, 且它們相互獨立,則它們的線性組合C1X1+C2X2+…+CnXn(Ci是不全為0的常數)仍然服""從常態分佈,且C1X1+C2X2+…+CnXn~N (∑Ciµi, ∑Ci^2σi^2)
統計學的應用
概念
樣本中各數據與樣本平均數的差的平方和的平均數叫做樣本方差;樣本方差的算術平方根叫做樣本標準差。
樣本方差和樣本標準差都是衡量一個樣本波動大小的量,樣本方差或樣本標準差越大,樣本數據的波動就越大。
方差和標準差。方差和標準差是測算離散趨勢最重要、最常用的指標。方差是各變數值與其均值離差平方的平均數,它是測算數值型數據離散程度的最重要的方法。標準差為方差的平方根,用S表示。標準差相應的計算公式為
標準差與方差不同的是,標準差和變數的計算單位相同,比方差清楚,因此很多時候我們分析的時候更多的使用的是標準差。
高考實例
(甘肅省,2002年)某校初三年級甲、乙兩班舉行電腦漢字輸入速度比賽,兩個班參加比賽的學生每分鐘輸入漢字的個數,經統計和計算後結果如下表所示:
| 班級 | 參加人數 | 平均字數 | 中位數 | 方差 |
| 甲 | 55 | 135 | 149 | 191 |
| 乙 | 55 | 135 | 151 | 110 |
有一位同學根據上表得出如下結論:
①甲、乙兩班學生的平均水平相同;
②乙班優秀的人數比甲班優秀的人數多(每分鐘輸入漢字達150個以上為優秀);
③甲班學生比賽成績的波動比乙班學生比賽成績的波動大.上述結論正確的是________(填序號).
解:填①、②、③,顯然①、③是正確的是.對於第②個結論,因為甲的中位數為149,表明甲班優秀人數未過半,而乙的中位數為151,表明乙班優秀人數在半數以上,故乙班優秀的人數比甲班優秀人數多,∴ ②正確.
切比雪夫不等式
定理
設隨機變數X就有數學期望E(X)=µ,方差D(X)=σ^2 ,則對於任意整數ε,有不等式
| 或 |
成立。
由切比雪夫不等式可以看出,若 ε 越小,則事件{|X-E(X)|< ε }的機率越大,即隨機變數X 集中在期望附近的可能性越大.
就只連續性隨機變數的情況來證明。
設X的概念密度為 f(x).
當方差已知時,切比雪夫不等式給出了r.v X與它的期望的偏差不小於3σ 的機率的估計式 .
如取ε =3σ
可見,對任給的分布,只要期望和方差D(X),則 r.v X取值偏離E(X)超過3σ 的機率小於0.111 .
應用實例
例9 已知正常男性成人血液中 ,每一毫升白細胞數平均是7300,均方差是700 . 利用切比雪夫不等式估計每毫升白細胞數在5200~9400之間的機率 .
解:設每毫升白細胞數為X
依題意,E(X)=7300,D(X)=7002
所求為 P(5200 ≤ X≤ 9400)
P(5200≤ X ≤ 9400)
= P(-2100 ≤X-E(X) ≤ 2100)
= P{ |X-E(X)| ≤ 2100}
由切比雪夫不等式,
即估計每毫升白細胞數在5200~9400之間的機率不小於8/9 .
| 關於「方差」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |