二項分布
| A+醫學百科 >> 二項分布 |
二項分布(
Binomial Distribution),即重複n次的伯努里試驗(Bernoulli Experiment),如果
1.在每次試驗中只有兩種可能的結果,而且是互相對立的;
2.每次實驗是獨立的,與其它各次試驗結果無關;
3.結果事件發生的機率在整個系列試驗中保持不變,則這一系列試驗稱為伯努力試驗.
在這試驗中,事件發生的次數為一隨機事件,它服從二次分布.二項分布可以用於可靠性試驗.可靠性試驗常常是投入n個相同的式樣進行試驗T小時,而只允許k個式樣失敗,應用二項分布可以得到通過試驗的機率.
若某事件機率為p,現重複試驗n次,該事件發生k次的機率為:P=C(k,n)×p^k×(1-p)^(n-k).C(k,n)表示組合數,即從n個事物中拿出k個的方法數.
目錄 |
醫學定義
在醫學領域中,有一些隨機事件是只具有兩種互斥結果的離散型隨機事件,稱為二項分類變數(dichotomous variable),如對病人治療結果的有效與無效,某種化驗結果的陽性與陰性,接觸某傳染源的感染與未感染等。二項分布(binomial distribution)就是對這類只具有兩種互斥結果的離散型隨機事件的規律性進行描述的一種機率分布。
考慮只有兩種可能結果的隨機試驗,當成功的機率(π)是恆定的,且各次試驗相互獨立,這種試驗在統計學上稱為貝努里試驗(Bernoulli trial)。如果進行n次貝努里試驗,取得成功次數為X(X=0,1,…,n)的機率可用下面的二項分布機率公式來描述:
P=C(X,n)*π^X*(1-π)^(n-X)
式中的n為獨立的貝努里試驗次數,π為成功的機率,(1-π)為失敗的機率,X為在n次貝努里試驗中出現成功的次數,表示在n次試驗中出現X的各種組合情況,在此稱為二項係數(binomial coefficient)。
所以的含義為:含量為n的樣本中,恰好有例陽性數的機率。
二項分布的應用條件
1.各觀察單位只能具有相互對立的一種結果,如陽性或陰性,生存或死亡等,屬於兩分類資料。
2.已知發生某一結果(陽性)的機率為π,其對立結果的機率為1-π,實際工作中要求π是從大量觀察中獲得比較穩定的數值。
3.n次試驗在相同條件下進行,且各個觀察單位的觀察結果相互獨立,即每個觀察單位的觀察結果不會影響到其他觀察單位的結果。如要求疾病無傳染性、無家族性等。
二項分布的性質
1.二項分布的均數和標準差在二項分布資料中,當π和n已知時,它的均數μ及其標準差σ可由式(7.3)和(7.4)算出。
μ=nπ(7.3)
σ=(7.4)
若均數和標準差不用絕對數表示,而是用率表示時,即對式(7.3)和(7.4)分別除以n,得
μp=π(7.5)
σp=(7.6)
σp是樣本率的標準誤的理論值,當π未知時,常用樣本率p作為π的估計值,式(7.6)變為:
sp= (7.7)
2.二項分布的累計機率(cumulative probability)常用的有左側累計和右側累計兩種方法。從陽性率為π的總體中隨機抽取含量為n的樣本,則
(1)最多有k例陽性的機率
(7.8)
(2)最少有k例陽性的機率
(7.9)
其中,X=0,1,2,…,k,…,n。
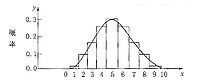
3.二項分布的圖形已知π和n,就能按公式計算X=0,1,…,n時的P(X)值。以X為橫坐標,以P(X)為縱坐標作圖,即可繪出二項分布的圖形,如圖7.1,給出了p=0.5和 p=0.3時不同n值對應的二項分布圖。
二項分布的形狀取決於π和n的大小,高峰在m=np處。當p接近0.5時,圖形是對稱的;p離0.5愈遠,對稱性愈差,但隨著n的增大,分布趨於對稱。當n→∞時,只要p不太靠近0或1,特別是當nP和n(1-P)都大於5時,二項分布近似於常態分佈。
π=0.5時,不同n值對應的二項分布
π=0.3時, 不同n值對應的二項分布
圖7.1二項分布示意
與兩點分布區別
兩點分布的分布列就是
X 0 1
P p 1-p
不論題目有什麼區別,只有兩種可能,要麼是這種結果要麼是那種結果,通俗點,要麼成功要麼失敗
而二項分布的可能結果是不確定的甚至是沒有盡頭的,
列一個項分布的分布列就是
X 0 1 2 ……… n
P C(0)(n).(1-p)^n C(1)(n).p.(1-p)^(n-1) …… C(n)(n).p^n.(1-p)^0
也就是說當n=1時,這個特殊二項分布就會變成兩點分布,
即兩點分布是一種特殊的二項分布
像一樓說的二項分布是兩點分布的多重實驗也不無道理,因為兩者都是獨立的重複實驗,只不過次數不同罷了
E(n) = np, var(n) = np(1-p) (n是實驗次數,p是每次實驗的機率)
| 關於「二項分布」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |