臨床生物化學/單室模型一級消除動力學

醫學電子書 >> 《臨床生物化學》 >> 治療藥物監測 >> 藥代動力學基礎及有關參數的應用 >> 單室模型一級消除動力學

臨床生物化學

治療藥物監測 藥代動力學基礎及有關參數的應用 藥動學模型 單室模型一級消除動力學 二室模型一級消除動力學 非線性動力學

臨床生物化學目錄

（一）單劑靜脈注射

⒈模式圖及藥-時關係單室模型的藥物可迅速在體內達到分布平衡，故可不考慮分布的影響。靜脈注射用藥時，藥物直接迅速進入血液，因此也不受吸收的影響。此時體內藥量將僅受包括生物轉化和排泄在內的消除影響，可建立如下模式圖。

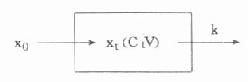
圖9-2 單室模型單劑靜脈注射模式圖

圖9-2中x₀為劑量，x_t為t時體內藥量，C_t表示t時的血藥濃度，V為表觀分布容積，k為消除速率常數。當按一級動力學方式消除時，體內藥量隨時間變化的微分方程為：

dx/dt＝－kX式⑴

積分得X＝X₀e^-kt式⑵

因體內藥量不可能直接測定，故引入比例常數：表觀分布容積V，以便用血藥濃度表示，即V＝X/C，所以X＝VC。代入式⑵可得

CC₀e^-kt式⑶

式⑶取對數得IgC＝IgC₀－kt/2.303式⑷

⑶和⑷式即為單室模型單劑靜脈注射給藥時的藥-時關係表達式。

⒉藥動學參數及計算

⑴藥-時關係表達式：從式⑷可看出，當血藥濃度以對數表示時，與時間t的關係為簡單的直線關係。因此，在靜脈注射藥物後不同時間取血，測定血藥濃度。根據血藥濃度對數值及相應時間，以圖解法或線性回歸法（最小二乘方法），即可求得如式⑷的直線方程（圖9-3）。

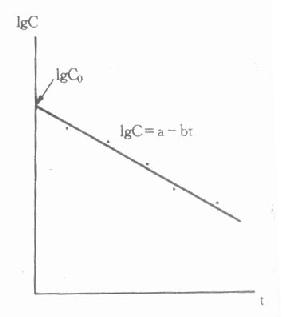
圖9-3 單劑靜脈注射血藥濃度－時間關係示意圖

IgC＝a－bt

此直線方程與縱軸的截距a＝IgC₀，故C₀＝Ig^-1a；而斜率b＝k/2.303，可計算出消除速率常數：

k＝2.303b。

⑵消除速率常數：消除速率常數（eliminationrateconstant，k）表示單位時間內機體能消除藥物的固定分數或百分比，單位為時間的倒數。如某藥的k＝0.2h^-1，表示機體每小時可消除該小時起點時體內藥量的20％，此即一級消除動力學的恆比消除特點。此時雖然單位時間消除的百分比不變，但隨著時間的推移，體內藥量逐漸減少，單位時間內消除的藥量也逐漸減少，而不是恆定不變的，消除速率常數是反映體內藥物消除快慢的一個重要參數。必須指出，一個藥物的消除速率常數在不同的個體間存在差異，但對同一個體來說，若無明顯的影響藥物體內過程的生理化、病理性變化，則是恆定的，並與該藥的劑型、給藥途徑、劑量（只要在一級動力學範圍內）無關。

⑶半壽期：藥動學中的半壽期（halflife，t_1/2）通常是指血漿消除半壽期，即血漿中藥物濃度下降一半所需要的時間。根據這一定義，當t＝t_1/2時，C₀＝2C，代入式⑷並整理可得

t_1/2＝0.693/k式⑸

從式⑸可看出，由於一級消除動力學時，k為一常數，半壽期亦為一常數。半壽期恆定不變，是一級消除動力學的又一特徵。和消除速率常數一樣，半壽期也是衡量藥物消除快慢的又一臨床常用參數，二者的關係如式⑸所表達。在藥物的臨床藥動學參數資料中，常告知半壽期，只要知道半壽期，根據式⑸即可求得消除速率常數k值。半壽期在指導用藥方案的制定中，有較大意義，將在後面討論。

⑷表現分布容積：如前所述，表觀分布容積（apparentvolumeofdistribution，V）是為了用血藥濃度計算體內藥量而引入的比例常數，表示假設體內藥物按血藥濃度均勻分布所需要的容積。前已談到藥物在體內分布可達動態平衡，但並非均勻一致，因此表觀分布容積僅是一理論容積，並不代表真實的解剖或生理空間。但只要知道某藥的表觀分布容積V，應用測定的血藥濃度，即可根據X_t＝C_t.V，計算得實際工作中無法測定的任一時刻體內的藥量，並可按上式計算出欲達某一血藥濃度C所需使用的劑量X＝CV。此外，表現分布容積還可用於評估藥物在體內的分布特點。人的總體液量約0.6L/kg體重，若某藥的V遠遠大於0.6L/kg體重，提示該藥主要分布於細胞內，被某組織、臟器主動攝取或對某些組織成分有特殊親和力，致使包括血漿在內的細胞外液中濃度低。大多數弱鹼性藥由於細胞內液比細胞外液偏酸而存在這一情況，如奎尼丁的表觀分布容積可超出2L/kg體重。反之，若某藥表觀分布容積遠遠低於0.6L/kg體重，則其主要分布於血漿等細胞外液中。多數弱酸性藥便是如此，如水楊酸的表觀分布容積僅0.2L/kg體重。

單室模型靜脈注射用藥時V的求算可採用外推法，即根據前面介紹的藥-時關係表達式求得t＝0時的C₀值及注射劑量X₀，按V＝X₀/C₀而計算出。其單位最常採用容積單位/kg體重。同前述藥動學參數一樣，V也是僅取決於藥物本身的理化性質、體內分布特點，而與該藥劑型、用藥方式、並在一級消除動力學範圍內與劑量都無關。在所有藥動學參數中，V和k是兩個最基本的參數。

⑸清除率：藥物清除率（clearance，Cl）是指單位時間內機體從血漿中消除某種藥物的總能力，其數值即等於該時間內機體能將多少體積血漿中的該藥完全消除。與k和t_1/2相同，Cl也是衡量體內藥物消除快慢的一個藥動學參數，但與k和t_1/2不同，Cl以具體的解剖生理學概念來表示，可更直觀形象地反映機體對藥物的消除能力。由於藥物在體內按血漿濃度分布的總體積為V，而k表示單位時間內藥物被消除的分數，故代表單位時間內機體能消除多少體積血漿藥物的清除率可按Cl＝Vk計算，單位為體積單位/時間單位。

⑹曲線下面積：血藥濃度-時間曲線與縱軸和橫軸間圍成的範圍面積即曲線下面積（areaundertheC-tcurve，AUC），單位為濃度單位×時間單位。由於任何藥物不論以何種劑型或途徑用藥，進入體內後，只要是同一種藥物分子，其消除均相同。因此AUC是評估進入體內藥量多少的一個客觀指標。在後面介紹的生物利用度的計算，以及近年建立的非模式消除動力學分析矩量法（statisticalmomenttheory）中，均有重要意義。

AUC的計算方法有稱重法、梯形法和積分法3種。其中稱重法為剪下曲線下紙片稱取重量，除以單位面積紙片的重量，即為該曲線的AUC。該法較不準確，現已少用。下面介紹後兩種計算方法。

1）梯形法：如圖9-4所示，可將曲線下範圍分做若干個等高梯形，分別計算各個梯形面積累加而成。即：

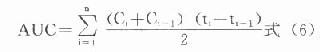
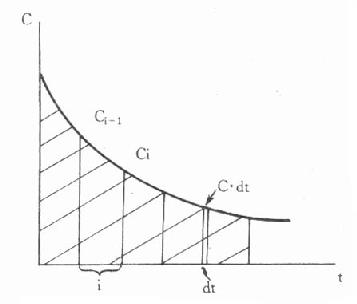
圖9-4 單劑靜脈注射時的藥-時曲線下面積

此法不論何種房室模型及何種途徑給藥均適用。但本法只能求算測定血藥濃度的時間範圍內的AUC。

2）積分法：當藥-時曲線按足夠小的時間間隔dt劃分時，可視做若干個矩形，每個矩形的面積分別為C.dt，將其積分得：

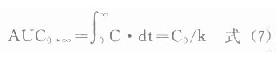
藥動學中積分法求算的AUC，均表示曲線隨時間無限外延，直至體內藥量完全消除時的面積。此外式⑺僅適用於單室模型、一級消除動力學單劑靜脈注射給藥的情況。

（二）恆速靜脈滴注

恆速靜脈滴注用藥，是臨床特別是危重症搶救中常用的方法。此時通過TDM工作，制定和調整滴注藥物速度，對確保搶救效果有重要意義。

⒈模式圖和藥-時關係表達式恆速靜脈滴注與單劑靜脈注射不同，此時藥物一方面以恆速的零級動力學方式進入體內，另一方面又以恆比的一級動力學方式從體內消除（圖9-5）。

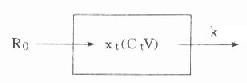
圖9-5 單室模型恆速靜脈滴注模式圖

圖中R₀為滴注速度，R₀＝X₀/t₀，X₀為t₀時間內滴注入體內的總藥量。余參數意義同圖9-2。此時體內藥量隨時間變化的微分表達式為：

dx/dt＝R₀－kX積分得X＝R₀/k(l-e^-kt)式⑻

或C＝R₀/Vk(l-e^-kt)式⑼

式⑻、⑼即為恆速靜脈滴注、單室模型一級消除動力學的體內藥量或血藥濃度隨時間變化的基本表達式。

⒉藥動學參數及計算

⑴穩態血藥濃度：穩態血藥濃度（steadystateplasmaconcentration，C_ss）指單位時間內自體內消除的藥量與進入體內的藥量相等時的血藥濃度。此時，血藥濃度將維持在坪值或波動在一定範圍內（多劑分次給藥時）。恆速靜脈滴注時，只要滴注速度R₀能使體內藥量保持在一級動力學消除範圍內，則當t→∞時，式⑼中e^-kt→0，式⑼可寫作

C_ss＝R₀/（k.V）式⑽

從式⑽可看出，由於k、V都是常數，恆速滴注時，R₀也不變，故此時血藥濃度亦為一常量，即達到穩態濃度。並且從式⑽還可看出，C_ss高低僅與R₀成正比。這也是只要滴注速度得當，長期靜脈恆速滴注，血藥濃度不會無限上升產生毒性反應的原因。此外，知道某藥的k、V值及達到治療作用所需的C_ss後，則可根據式⑽計算出所需的滴注速度R₀＝C_ss.k.V，需指出的是，當恆速靜脈滴注藥物用於搶救心衰或休克病人時，隨著血流動力學的改善，病人的k及V均可改變，必須通過TDM及時調整滴注速度，以保持在所需的C_ss。

若將時間用半壽期數n表示，即t＝nt_1/2＝0.693n/k，應用前面學過的公式，可得到達穩態前血藥濃度C與C_ss的關係：

C＝C_ss［1－（1/2）ⁿ］式⑾

從式⑾可計算出恆速靜脈滴注經過5個半壽期，血藥濃度可達C_ss的96.8％，6個半壽期達98.4％。因此，臨床上通常視恆速靜脈滴注經過5-6個半壽期後，達到了穩態血藥濃度。

⑵靜脈滴注的負荷劑量：從上可知，為達C_ss，至少需恆速靜脈滴注5-6個半壽期以上。而臨床搶救中常需迅速達到有效血藥濃度，此時可考慮使用負荷劑量法。負荷劑量（loadingdose，D）是為了迅速或立即達到穩態濃度而首先使用的增大劑量。靜脈滴注用藥時，有下面兩種負荷劑量法。

1）先靜脈注射一負荷劑量，立即達C_ss，繼之以恆速滴注維持。根據前面所學知識可得D＝C_ss.V＝R₀/k。故根據治療濃度確定的所需C_ss和該藥的V，或為達所需C_ss計算出的恆速滴注速度R₀和該藥的k，即可按上式求得所需D，靜脈推注後，立即改為R₀速度恆速滴注，便可立即達到C_ss並維持之。

2）先快速滴注t時間，迅速達所需C_ss水平，再改為恆定的慢速滴注維持。此法較上法安全，尤適用於毒性大、治療濃度與中毒濃度接近的藥物。此時可根據下式（推導從略）計算出所需的負荷速度R₀^*：

R₀^*＝R₀/l-e^-kt式⑿

式中R₀為達所需C_ss計算出的恆定慢速滴注速度，t為計劃的負荷滴注時間。按R₀^＊滴注t時間後，血藥濃度即可迅速升至C_ss水平，調整滴注速度為R₀，即可維持在C_ss水平。

⑶其它藥動學參數計算：若已知某藥其它方式用藥時的有關藥動學參數，前已述及也可用於恆速靜脈滴注。當需通過恆速靜脈滴注計算藥動學參數，可使用終止滴定法。即在恆速靜脈滴注t時間後，停止滴注，以t時間為零時，測定隨後幾個不同的時點（t』）的血藥濃度，同前靜脈注射法求得直線方程：

IgC_t＝

應注意此式的t為開始滴注到停止滴注的時間。然後根據下列各式：

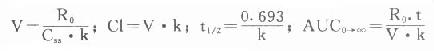
分別計算出各有關藥動學參數。

（三）血管外單劑用藥

⒈模式圖和藥-時關係表達式口服、肌肉或皮下注射用藥時，和前面討論的血管內給藥不同。此時即存在藥物從用藥部位吸收進入血液的過程，也存在藥物自體內（血液）消除的影響。由於絕大多數藥物均是以被動轉運的方式吸收，故上述兩個過程都按一級動力學方式進行。其模式圖如下（圖9-6）：

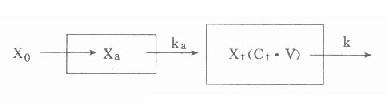
X_a：t時吸收部位藥量

K_a：吸收速率常數其它參數同圖9-3

圖9-6 血管外用藥模式圖

根據上述關係及模式圖，可建立如下微分方程組：

dx_a/dt=-K_a.X_a（吸收部位藥物衰減速率）

dx_a/dt=-K_a.X_a--K.X（血液等藥物分布室內藥物衰減速率）

解此微分方程組得

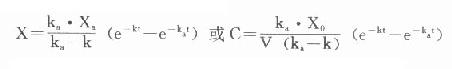
若考慮口服時吸收不完全而引入吸收分數F，則：

式⒀即為單劑血管外用藥時，血管濃度隨時間變化的基本表達式。

⒉藥動學參數及計算通過血管外用藥計算藥動學參數多用殘數法（methodofresidual）。該法基本指導思想是，以血管外用藥能獲治作用的藥物，必然K_a＞＞k，才有可能在體內達到治療血藥濃度，因此，當t足夠大時，首先e^-kat→0此時式⒀可寫作：

C＝A.e^-kt取對數得lgC＝lgA－kt/2.303

也就是說單劑血管外用藥時，經過一段時間後，其血藥濃度的變化可視做只受消除的影響，即進入消除相（圖9-7）。

此時按前面介紹的單劑靜脈注射藥動學參數計演算法，可求得A、k和消除t_1/2。而在進入消除相以前的時間內，血藥濃度為吸收和消除兩因素共同作用的結果。若將式⒀展開移項則得

A.e^-kt-C=A.e^-kat,令C_r=A.e^-kt-C,

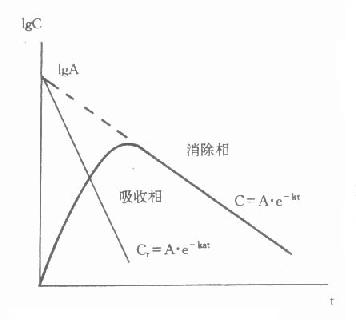
圖9-7 單劑血管外用藥血藥

濃度-時間關係及藥動力學求算示意圖

Cr為消除相外推段某時點血藥濃度減去該時點實測濃度的殘數或差值（注意不是對數值相減）。則：

C_r=A.e-k_at，取對數得TgC_r＝IgA－k_at/2.303

此即分布相藥-時關係的表達式（圖9-6），同理可求算得k_a和吸收t_1/2。

在計算其它藥動學參數時，反映藥物被機體吸收利用程度的吸收分數F，即生物利用度（bioavailability）是必須首先先知道的。血管外注射用藥時，一般均視為F＝1。而現在多數口服藥在說明書中已告知F值，否則需根據某藥口服時AUC與該藥同劑量靜脈注射時的AUC相比計算出。口服時的AUC可用前述梯形法，或按下列積分法公式求得：

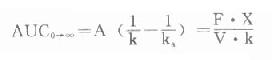
其他藥動學參數計算見下。

⑴表觀分布容積：

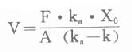
⑵清除率：Cl＝k.V

⑶達峰時間（timeofthepeakconcentration，t_p）：即血管外給藥時，達到最高濃度所需時間。由於在此時，血藥濃度變化速率dC/dt＝0，故可推導出：

⑷峰濃度（maximumconcentration，C_max）：將t_p代入式⒀可得：

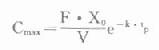
（四）多次用藥

為保持或鞏固療效，臨床常需反覆多次較長期用藥。此時體內藥量或血藥濃度將出現如圖9-8所示的波動式上升，每次用藥間隔中出現從峰值向谷值的變化。若體內藥量不超過一級消除動力學範圍，隨著用藥次數增多，血藥濃度逐漸升高，但最終將穩定在一定範圍內波動，即進入穩態濃度（推導見後）。指導合理的多次用藥方案的制定和調整，使穩態血藥濃度波動在治療濃度範圍內，是TDM在臨床治療學中最主要的任務。下面我們將介紹按恆定劑量、固定間隔時間多次用藥時與TDM有關的藥動學知識。需要指出的是，單劑用藥時的有關藥動學參數仍適用於多劑給藥，並且是多劑用藥藥動學的基礎。

⒈ 劑量函數當按恆量固定間隔時間τ多次用藥，無論是靜脈注射，還是肌肉注射、口服等血管外用藥，均可推導得多劑量函數r（推導從略）。

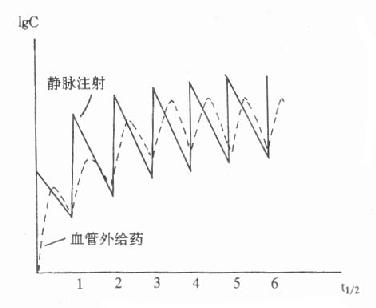
圖9-8 多劑用藥的血藥濃度-時間關係示意圖

n：用藥次數

K_i：有關速率常數

多劑量函數為多劑用藥時，用藥間隔時間τ和用藥次數n對體內藥量或血藥濃度的影響的通用函數表達式。具體應用時，只需將單劑用藥有關公式中含有速率常數的指數或對數項乘以多劑量函數r即可。但要注意：①此時多劑量函數r中的k_i均應換成該項之k或k_a；②對數項時，多劑量函數r應放在對數內與有關速率常數相乘；③相應各公式中t應為第n次用藥後的時間。如此根據⑶式可得多劑靜脈注射用藥時，藥-時關係表達式為：

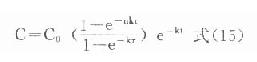
同理根據式⒀可得血管外多劑用藥的藥-時關係表達式為：

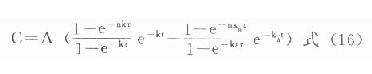
恆速靜脈滴注時＝0，仍用原式

⒉穩態濃度和平均穩態濃度當連續多次給藥後，n足夠大時，多劑量函數式中，則

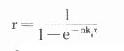
顯然此時的多劑量函數式為一常量，此即穩態時的多劑量函數式。分別代入式⒂或⒃中可得：

靜脈注射時：

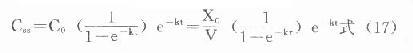
血管外給藥時：

以上兩式中，由於僅時間t在每次用藥間隔中從0→τ的範圍變化，血藥濃度都將進入在每次用藥間隔中，恆定在一定範圍內波動的穩態狀態。τ越大，波動範圍越大。式⒄、⒅則分別為靜脈注射、血管外用藥時，穩態濃度在每次用藥間隔中隨時間變化的表達式。實際工作中，當nτ＝6t_1/2時，血藥濃度可達穩態濃度的98.4％。故在連續多劑用藥時，一般認為經過6個半壽期以上，即可視做已達穩態狀態。此外，無論達穩態否，如果變換劑量，必須再經過6個半壽期以上始能進入新的穩態。

靜脈注射時，每次間隔中波動的峰值總是在每次注射完的瞬間（t＝0），而谷值則在下次注射前（t＝τ）出現，分別代入⒄式可得靜脈注射多劑用藥時

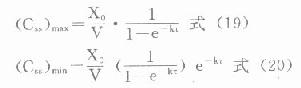
血管外給藥時，每次間隔中，谷濃度也將在下次給藥前。但由於存在吸收，峰濃度將在達峰時間（t』_p）出現。將穩態時多劑量函數代入前述單劑用藥t_p，求算公式得：

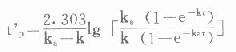
分別以上述t』_p或t＝τ代入⒅式，並且因k_a較大，令e-kaτ→0,可推得血管外給藥的

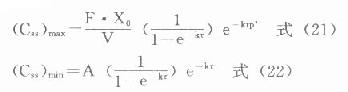
在TDM工作中，運用式⒆-(22)式，選定間隔時間（τ），計算劑量，或選定劑量計算nt-family:TimesNewRoman;mso-fareast-font-family:宋體;mso-font-kerning:1.0pt;mso-ansi-language:EN-US;mso-fareast-language:ZH-CN;mso-bidi-language:AR-SA"lang="EN-US">τ，使（C_ss）_max＜最小中毒濃度，而（C_ss）_min＞最小有效濃度，是十分有用且經常性的工作。

平均穩態血藥濃度（

）為穩態時，兩劑用藥間藥-時曲線下面積（AUC）除以間隔時間τ的商值。必須注意，（

）不是（C_ss）_max和（C_ss）_min的算術或幾何平均值。根據穩態濃度的定義可知，此時兩劑間AUC就為該劑量單劑給藥時的AUC_0→∞。根據前面學過的公式，可得

靜脈注射：

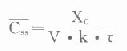
血管外用藥：

在TDM工作中，對給藥間隔τ不是遠遠長於半壽期，即穩態時血藥濃度波動範圍不是太大，且有效血藥濃度範圍上限與最小中毒濃度有一定差距的藥物，以有效血藥濃度範圍中值或略低定為

，按上式公式制定或調整用藥方案，是一簡便並且為臨床所能接受的方法。

⒊負荷劑量上面討論中談到，多劑用藥時，無論間隔時間長短，都需經過6個以上半壽期才可認為已達穩態。對t_1/2較長或急需迅速發揮療效的藥物，往往需要使用負荷劑量（X₀^*）。多劑用藥時欲使第一次用藥後即達到穩態濃度，負荷劑量可按下面公式計算（推導從略）。

靜脈注射

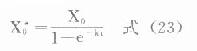
血管外用藥

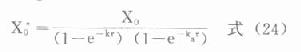
式中X₀為擬使用的固定劑量。若吸收較快，即k_a大，e-kaτ→0,(24)式也可寫做

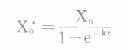
上述各式中1/（1－e^-kτ）即前述穩態時的多劑函數式，亦稱蓄積指數（accumulationindex），代表穩態時血藥濃度峰值或谷值與首劑用藥時峰值或谷值之比。蓄積指數實際上反映了達穩態後，每次給藥間隔中任一時點血藥濃度為首劑用藥後同一時點血藥濃度的倍數。如τ＝t_1/2時，蓄積指數為2，X₀^*＝2X₀。實際工作中，根據所需穩態血藥濃度水平確定的X₀及τ，按上述公式計算出負荷劑量X₀^*首劑使用後，再按X₀及τ，恆量固定間隔用藥，可在負荷劑量使用後即達穩態濃度並維持之，獲得迅速而穩定的療效。

藥動學模型 | 二室模型一級消除動力學

關於「臨床生物化學/單室模型一級消除動力學」的留言：	訂閱討論RSS
目前暫無留言
添加留言

更多醫學百科條目