臨床生物化學/非線性動力學
| 醫學電子書 >> 《臨床生物化學》 >> 治療藥物監測 >> 藥代動力學基礎及有關參數的應用 >> 非線性動力學 |
| 臨床生物化學 |
|
|
在消除動力學模型中已介紹，當體內藥量（血藥濃度）超過機體最大消除能力時，將為恆量消除的零級動力學，而藥量（血藥濃度）降至最大消除能力以下，將轉化為恆比消除的一級動力學（圖9-11）。這種存在動力學轉換的情況下，藥物的消除不能用一種統一簡單的線性過程描述，故稱非線性動力學（nonlinearpharmacokinetics）消除。若某藥使用的劑量能使其在體內的消除由一級動力學轉為零級，繼續使用該劑量，血藥濃度將會出現持續上升，而不能達到穩態濃度。對於安全範圍狹窄的藥物出現這種情況，是十分危險的。在需進行TDM的藥物中，苯妥英鈉、氨茶鹼等在常用治療劑量下就存在這種情況。
造成這種藥動學方式轉化的原因，主要是體內藥量（血藥濃度）超過了機體生物轉化酶系的最大催化能力，即出現了飽和代謝，故亦常用描述酶促反應動力學的米氏方程表達非線性動力學消除的速率，即
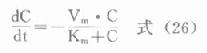
式中Vm為最大消除速率，Km為米氏常數，相當於恰可產生Vm/2時的藥物濃度。當C＜＜Km時，式(26)可變為
dc/dt=VmKm,令0k=Vmdc/kmdt,則dc/dt=-kC
此即前面已介紹的典型一級消除動力學微分表達式。而當C＞＞Km時，式(26)可寫作
dC/dt=-Vm
上式為典型的零級消除動力學微分表達式。
由式(26)可推導得非線性動力學消除時的有關藥動學參數計算公式：
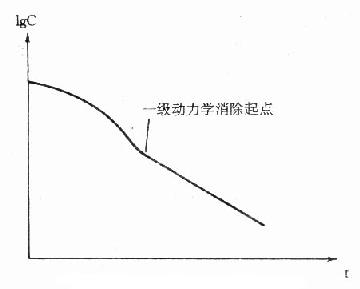
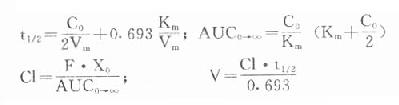
圖9-11 非線性動力學消除血藥濃度-時間關係示意圖
從上述各式中可看出，非線性消除動力學藥物的多數參數均為隨藥物濃度而變化的變數，並非常數。在非線性動力學消除的藥物TDM工作中，Vm和Km是兩個十分有用的基本常數。必須注意的是，在藥物體內過程中，生物轉化能力影響因素多，個體差異尤為顯著，因此Vm和Km個體差異大。在應用這兩個參數的群體均值制定的劑量方案，往往不能達到預期效果。對於需長期用藥或完全範圍窄的藥物，按下面方法確定具體個體的Vm和Km值實屬必要。
不同時點取血測定血藥濃度，依次求得相鄰時點血藥濃度及時間差值△C和△t。將式(26)中的dC/dt視做△C/△t，即消除速率V，而以相應兩時點血藥濃度均值C作為產生相應速率改變的濃度，分別代入式(26)，並取倒數整理得：
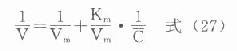
式(27)為1/V隨1/C變化的直線方程（圖9-12）。該直線與縱軸交點為1/Vm，斜率為Vm/Km，故可分別求出Vm和Km。
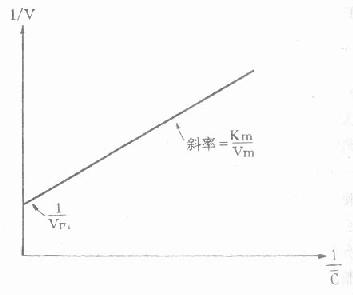
圖9-12 雙倒數法求算非線性動力學消除的Vm和Km示意圖
根據非線性動力學消除的特點，多劑用藥時，只有當藥物進入體內的速率R（量/d）恰與藥物自體內的消除速率相等時，才有可能達穩態濃度Css。借用式(26)可得
R＝Vm.Cm/Km+Cm式(28)
由此可得Css＝Km.R/Vm-R式(29)
由上兩式可計算出非線性動力學消除的藥物，欲達某穩態濃度所需的用藥速率（每日用藥量），或按某速率用藥時所能達到的穩態濃度，在這類藥物的TDM工作中極為有用。從式(28)、(29)中也可看出，Vm和Km是必須首先求算出的基礎。
 二室模型一級消除動力學 | 合理使用治療藥物監測應考慮的基本因素  |
| 關於「臨床生物化學/非線性動力學」的留言： |  訂閱討論RSS
|
|
目前暫無留言 | |
| 添加留言 | |