臨床生物化學/二室模型一級消除動力學

醫學電子書 >> 《臨床生物化學》 >> 治療藥物監測 >> 藥代動力學基礎及有關參數的應用 >> 二室模型一級消除動力學

臨床生物化學

治療藥物監測 藥代動力學基礎及有關參數的應用 藥動學模型 單室模型一級消除動力學 二室模型一級消除動力學 非線性動力學

臨床生物化學目錄

多室模型和前面討論的單室模型不同，此時存在著由包括血液在內的中央室向周邊室分布達到平衡的過程，影響血藥濃度的因素更為複雜，下面以單劑靜脈注射為例，簡介有關藥動學知識。

（一）模式圖和藥-時關係

靜脈注射時，不存在吸收過程，中央室中的藥量或血藥濃度受中央室與周邊室間雙向分布，以及自中央室消除的影響。其模式如圖9-9所示。

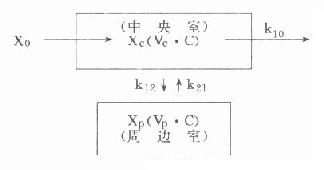
x_c中央室藥量

x_p周邊室藥量

v_c中央室分布容積

v_p周邊室分布容積

k₁₀中央室向周邊室轉運速率常數

k₂₁周邊室向中央室轉運速率常數

圖9-9 二室分布靜脈注射模式圖

中央室藥量變化的速率微分方程為：

dk_c/dt=k₂₁.x_p-k₂₁.x_c-k₁₀.x_c

對上式積分並引入中央室分布容積Vc，可得中央室（血）藥物濃度隨時間變化的基本表達式：

C＝A.e＋B.e^-βt式(25)

式中α為分布速率常數，β為消除速率常數，A、B為經驗常數。四者都是由模式參數k₁₀、k₁₂、k₂₁組成的混雜參數（hybridparameters）。存在：

α.β＝k₂₁.k₁₀α＋β＝k₁₀＋k₁₂＋k₂₁

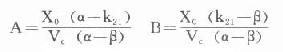
（二）藥動學參數計算

二室模型靜脈注射藥動學參數的求算，類似於單室模型血管外用藥，仍採用殘數法。即因為α＞β,當t充分大時，A.e^-αt→0，則式(25)變為

C＝Be^-βt

此即消除相藥-時關係表達式。按前述方法可求得B、β和消除半壽期t_1/2β。將式(25)移項可得：

C－B.e^-αt＝A.e^-αt

令C_r＝C－B.e^-βt，C_r即為消除相以前某時點實測血藥濃度減去消除相該點外推濃度的殘數。代入上式可得分布相藥-時關係表達式

C_r＝A.e^-αt

同樣可求得A、α和分布半壽期t_1/2α（圖9-10）。

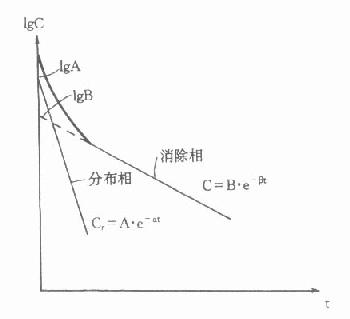
圖9-10 二室模型靜脈注射血藥濃度-時間關係示意圖

再根據下列公式，可求得各有關藥動學參數。

中央室表觀分布容積：Vc＝X₀/（A＋B）

周邊室向中央室的轉運速率常數：

自中央室消除的速率常數：

k₁₀＝α.β/k₂₁

中央室向周邊室轉運的速率常數：

k₁₂＝（α＋β）－（k₁₀＋k₂₁）

曲線下面積：AUC_0→∞＝A/α+B/β（積分外推法）

周邊室表觀分布容積：V_p＝V_c.k₁₂/k₂₁

總表觀分布容積：

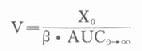表示體內藥量按消除相血藥濃度分布的容積）

穩態表觀分布容積：V_ss＝V_c＋V_p

消除率：Cl＝k₁₀.V_c＝β.V

血管外用藥時，由於存在吸收因素，求算藥動學參數的基本方法仍為殘數法，但此時需進行兩次殘數處理。有關二室模型血管外用藥及二室以上多室模型的藥動學，在TDM的實際工作中很少應用，可參閱有關藥動學專著。

單室模型一級消除動力學 | 非線性動力學

關於「臨床生物化學/二室模型一級消除動力學」的留言：	訂閱討論RSS
目前暫無留言
添加留言

更多醫學百科條目