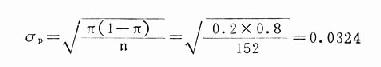預防醫學/率的假設檢驗——正態近似法

醫學電子書 >> 《預防醫學》 >> 計數資料分析 >> 率的假設檢驗——正態近似法

預防醫學

計數資料分析 相對數的常用指標 應用相對數時的注意事項 率的標準化法 率的抽樣誤差和總體率的估計 率的假設檢驗——正態近似法 x2檢驗

預防醫學目錄

一、樣本率與總體率的比較

觀察樣本數較大時，樣本率的頻數分布近似常態分佈，可應用常態分佈的規律性檢驗率的差異顯著性。其公式為：

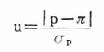公式（20.7）

式中p為樣本率，π為總體率，σ_p為根據總體率計算的標準誤。由於u服從常態分佈，故可用表20-10作判斷。

表20-10　｜u｜值、P值與統計結論

｜u｜值	P值	統計結論
＜1.96	＞0.05	不拒絕H0，差異無統計學意義
≥1.96	≤0.05	拒絕H0，接受H1，差異有統計學意義
≥2.58	≤0.01	拒絕H0，接受H1，差異有高度統計學意義

例20.6根據以往經驗，一般潰瘍病患者中有20%發生胃出血症状。某醫生觀察65歲以上潰瘍病人152例，其中48例發生胃出血症状，問老年患者出血情況與一般患者有無不同？

按慣例大量觀察所得的率可當作總體率看待，則本例總體率π為0.2(20%)，1-π=0.8，n=152

標準誤差

樣本率p=48/152×100%=31.6%=0.316

檢驗步驟：

1．建立檢驗假設：

H₀:π=π₀^＝0.2

H1:π≠π0

α=0.05

2.計算u值（按公式20.7）

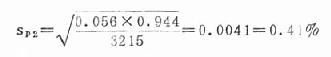
u＜2.58,P＜0.01,差異有高度統計學意義

按 α=0.05水準拒絕H0，故可以認為老年潰瘍病患者較易於發生胃出血，與一般患者有所不同。

二、兩個樣本率差異的意義檢驗

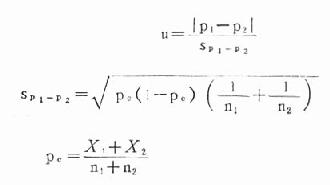
公式（20.8）

公式（20.9）

公式（20.10）

以上公式中：P₁，P₂為兩個樣本率

p_c為合併樣本率

X₁和X₂分別為兩樣本陽性例數

如果兩個樣本都相當大，則s_p1-p2改用下式計算

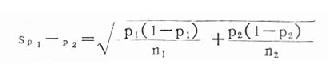
公式（20.11）

現仍以上述計算率的標準誤的例題，進一步檢驗兩個樣本率差異有無意義。

基本資料：n₁=3315,p₁=1.78%=0.0178,1-p₁=0.9822

n₂=3215,p₂=5.60%=0.056,1-p₂=0.944

檢驗步驟：

1．建立檢驗假設：

H₀：π₁=π₂

H₁:π₁≠π₂

α=0.05

2．計算u值：因兩個都是大樣本，故採用公式（20.11）以求s_p1-p2

3．確定P值和分析：本題u=8.234＞2.58,P＜0.01，差異有高度統計學意義，按α=0.05水準拒絕H₀，可以認為水中碘濃度高的居民甲狀腺患病率高於水中碘濃度低的居民。

率的抽樣誤差和總體率的估計 | x2檢驗

關於「預防醫學/率的假設檢驗——正態近似法」的留言：	訂閱討論RSS
目前暫無留言
添加留言

更多醫學百科條目