預防醫學/率的抽樣誤差和總體率的估計
| 醫學電子書 >> 《預防醫學》 >> 計數資料分析 >> 率的抽樣誤差和總體率的估計 |
| 預防醫學 |
|
|
|
一、率的標準誤
用抽樣方法進行研究時,必然存在抽樣誤差。率的抽樣誤差大小可用率的標準誤來表示,計算公式如下:
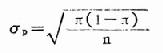 公式(20.5)
公式(20.5)
式中:σp為率的標準誤,π為總體陽性率,n為樣本含量。因為實際工作中很難知道總體陽性率π,故一般採用樣本率p 來代替,而上式就變為
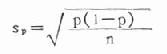 公式(20.6)
公式(20.6)
例 20.5河北省組織高碘地方性甲狀腺腫流行病學調查,作者調查了飲用不同碘濃度井水居民甲狀腺腫的患病情況,其中有兩組資料如下表,試分別求出率的標準誤。
| 水中含碘量均數(μg/L) | 受檢人數 | 患病人數 | 患病率(%) |
| 458.25 | 3315 | 59 | 1.78 |
| 825.95 | 3215 | 180 | 5.60 |
計演算法:第一組:n1=3315,p1=1.78%=0.0178
1-p1=1-0.0178=0.9822
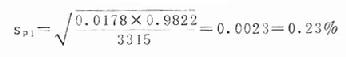
第二組:n2=3215,p2=5.60%=0.056
1-p2=1-0.056=0.944
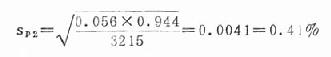
二、總體率的可信區間
由於樣本率與總體率之間存在著抽樣誤差,所以也需根據樣本率來推算總體率所在的範圍,根據樣本含量n和樣本率P的大小不同,分別採用下列兩種方法:
(一)正態近似法
當樣本含量n足夠大,且樣本率P和(1-p)均不太小,如np或n(1-p)均≥5時,樣本率的分布近似常態分佈,則總體率的可信區間可由下列公式估計:
總體率(π)的95%可信區間:p±1.96sp
總體率(π)的99%可信區間:p±2.58sp
例如前述兩組高碘地方性甲狀腺腫患病率的總體患病率可信區間為:
第一組:
95%可信區間為1.78%±1.96×0.23%=1.33%~2.23%
95%可信區間為1.78%±2.58×0.23%=1.19%~2.37%
第二組:
95%可信區間為5.6%±1.96×0.41%=4.80%~6.40%
95%可信區間為5.6%±2.58×0.41%=4.54%~6.66%
(二)查表法
當樣本含量n較小,如n≤50,特別是p接近0或1時,則按二項分布原理確定總體率的可信區間,其計算較繁,讀者可根據樣本含量n和陽性數X參照專用統計學介紹的二項分布中95%可信限表。
| 關於「預防醫學/率的抽樣誤差和總體率的估計」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |