預防醫學/x2檢驗

醫學電子書 >> 《預防醫學》 >> 計數資料分析 >> x2檢驗

預防醫學

計數資料分析 相對數的常用指標 應用相對數時的注意事項 率的標準化法 率的抽樣誤差和總體率的估計 率的假設檢驗——正態近似法 x2檢驗

預防醫學目錄

x²檢驗（chi-square test）或稱卡方檢驗，是一種用途較廣的假設檢驗方法。可以分為成組比較（不配對資料）和個別比較（配對，或同一對象兩種處理的比較）兩類。

目錄 1 一、四格表資料的x2檢驗 2 二、四格表的專用公式 3 三、四格表x2值的校正 4 四、行×列表的卡方檢驗（x2testfor R×C table） 5 五、配對計數資料x2檢驗（x2testof paired comparison of enumeration data）

一、四格表資料的x²檢驗

例20.7某醫院分別用化學療法和化療結合放射治療卵巢癌腫患者，結果如表20-11，問兩種療法有無差別？

表20-11 兩種療法治療卵巢癌的療效比較

組別	有效	無效	合計	有效率（%）
化療組	19	24	43	44.2
化療加放療組	34	10	44	77.3
合計	53	34	87	60.9

表內用虛線隔開的這四個數據是整個表中的基本資料，其餘數據均由此推算出來；這四格資料表就專稱四格表（fourfold table），或稱2行2列表（2×2 contingency table）從該資料算出的兩種療法有效率分別為44.2%和77.3%，兩者的差別可能是抽樣誤差所致，亦可能是兩種治療有效率（總體率）確有所不同。這裡可通過x²檢驗來區別其差異有無統計學意義，檢驗的基本公式為：

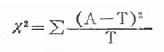公式（20.12)

式中A為實際數，以上四格表的四個數據就是實際數。T為理論數，是根據檢驗假設推斷出來的；即假設這兩種卵巢癌治療的有效率本無不同，差別僅是由抽樣誤差所致。這裡可將兩種療法合計有效率作為理論上的有效率，即53/87=60.9%，以此為依據便可推算出四格表中相應的四格的理論數。茲以表20-11資料為例檢驗如下。

檢驗步驟：

1．建立檢驗假設：

H₀：π₁=π2

H1:π1≠π2

α=0.05

2．計算理論數（T_RC），計算公式為：

T_RC=n_R.n_c/n公式（20.13）

式中T_RC是表示第R行C列格子的理論數，n_R為理論數同行的合計數，n_C為與理論數同列的合計數，n為總例數。

第1行1列： 43×53/87=26.2

第1行2列： 43×34/87=16.8

第2行1列： 44×53/87=26.8

第2行2列： 4×34/87=17.2

以推算結果，可與原四項實際數並列成表20-12：

表20-12 兩種療法治療卵巢癌的療效比較

組別	有效	無效	合計
化療組	19(26.2)	24(16.8)	43
化療加放療組	34（26.8）	10(17.2)	44
合計	53	34	87

因為上表每行和每列合計數都是固定的，所以只要用T_RC式求得其中一項理論數（例如T_1.1=26.2），則其餘三項理論數都可用同行或同列合計數相減，直接求出，示範如下：

T_1.1=26.2

T_1.2=43-26.2=16.8

T_2.1=53-26.2=26.8

T_2.2=44-26.2=17.2

3.計算x²值 按公式20.12代入

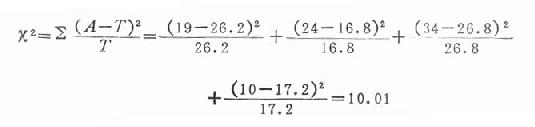
4．查x²值表求P值

在查表之前應知本題自由度。按x²檢驗的自由度v=（行數-1）（列數-1），則該題的自由度v=（2-1）（2-1）=1，查x²界值表（附表20-1），找到x²_0.001(1)=6.63,而本題x²=10.01即x²＞x²_0.001(1),P＜0.01，差異有高度統計學意義，按α=0.05水準，拒絕H₀，可以認為採用化療加放療治療卵巢癌的療效比單用化療佳。

通過實例計算，讀者對卡方的基本公式有如下理解：若各理論數與相應實際數相差越小，x²值越小；如兩者相同，則x²值必為零，而x²永遠為正值。又因為每一對理論數和實際數都加入x²值中，分組越多，即格子數越多，x²值也會越大，因而每考慮x²值大小的意義時同時要考慮到格子數。因此自由度大時，x²的界值也相應增大。

二、四格表的專用公式

對於四格表資料，還可用以下專用公式求x²值。

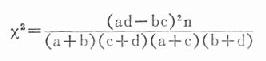公式（20.14）

式中a、b、c、d各代表四格表中四個實際數，現仍以表20-12為例，將上式符號標記如下（表20-13），並示範計算。

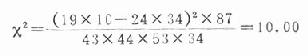
表20-13 兩種療法治療卵巢腫瘤患者的療效

組別	有效	無效	合計
化療組	19(a)	24(b)	43(a+b)
化療加放療組	34(c)	10(d)	44(c+d)
	53(a+c)	34(b+d)	87(n)

計算結果與前述用基本公式一致，相差0.01用換算時小數點後四捨五入所致。

三、四格表x²值的校正

x²值表是數理統計根據常態分佈中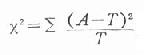 的定義計算出來的。 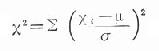只是一種近似，在自由度大於1、理論數皆大於5時，這種近似很好；當自由度為1時，尤其當1＜T＜5，而n＞40時，應用以下校正公式：

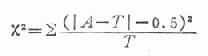公式（20.15）

如果用四格表專用公式，亦應用下式校正：

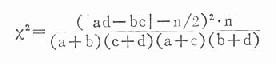公式（20.16）

例20.8某醫師用甲、乙兩療法治療小兒單純性消化不良，結果如表20-14。試比較兩種療法效果有無差異？

表20-14 兩種療法效果比較的卡方較正計算

療法	痊癒數	未愈數	合計
甲	26(28.82)	7(4.18)	33
乙	36(33.18)	2(4.82)	38
合計	62	9	71

從表20-14可見，T_1.2和T_2.2數值都＜5，且總例數大於40，故宜用校正公式（20.15）檢驗。步驟如下：

1．檢驗假設：

H₀：π₁=π₂

H₁:π₁≠π₂

α=0.05

2.計算理論數:(已完成列入四格表括弧中)

3.計算x²值：應用公式（20.15）運算如下：

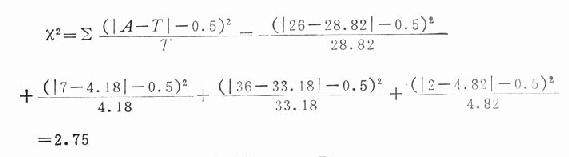
查x²界值表，x²_0.05(1)=3.84,故x²＜x²_0.05(1),P＞0.05.

按α=0.05水準，接受H₀，兩種療效差異無統計學意義。

如果不採用校正公式，而用原基本公式，算得的結果x²=4.068，則結論就不同了。

如果觀察資料的T＜1或n＜40時，四格表資料用上述校正法也不行，可參考預防醫學專業用的醫學統計學教材中的精確檢驗法直接計算機率以作判斷。

四、行×列表的卡方檢驗（x²testfor R×C table）

適用於兩個組以上的率或百分比差別的顯著性檢驗。其檢驗步驟與上述相同，簡單計算公式如下：

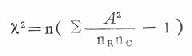公式（20.17）

式中n為總例數；A為各觀察值；n_R和n_C為與各A值相應的行和列合計的總數。

例20.9北方冬季日照短而南移，居宅設計如何適應以獲得最大日照量，增強居民體質，減少小兒佝僂病，實屬重要。胡氏等1986年在北京進行住宅建築日照衛生標準的研究，對214幢樓房居民的嬰幼兒712人體檢，檢出輕度佝僂病333例，比較了居室朝向與患病的關係。現將該資料歸納如表20-15作行×列檢驗。

表20-15居室朝向與室內嬰幼兒佝僂病患病率比較

檢查結果	居室朝向				合計
	南	西、西南	東、東南	北、東北、西北
患病	180	14	120	65	379
無病	200	16	84	33	333
合計	380	30	204	98	712
患病率(%)	47.4	46.7	58.8	66.3	53.2

該表資料由2行4列組成，稱2×4表，可用公式（20.17）檢驗。

（一）檢驗步驟

1．檢驗假設

H₀：四類朝向居民嬰幼兒佝僂病患病率相同。

H₁：四類朝向居民嬰幼兒佝僂病患率不同。

α=0.05

2．計算x²值

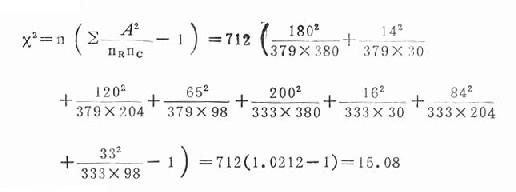
3．確定P值和分析

本題v=（2-1）（4-3）=3，據此查附表20-1：

x²_0.01(3)=11.34,本題x²=15.08,x²＞x²_0.01(3),P＜0.01,按α=0.05水準，拒絕H₀，可以認為居室朝向不同的居民，嬰幼兒佝僂病患病率有差異。

（二）行×列表x²檢驗注意事項

1．一般認為行×列表中不宜有1/5以上格子的理論數小於5，或有小於1的理論數。當理論數太小可採取下列方法處理：①增加樣本含量以增大理論數；②刪去上述理論數太小的行和列；③將太小理論數所在行或列與性質相近的鄰行鄰列中的實際數合併，使重新計算的理論數增大。由於後兩法可能會損失信息，損害樣本的隨機性，不同的合併方式有可能影響推斷結論，故不宜作常規方法。另外，不能把不同性質的實際數合併，如研究血型時，不能把不同的血型資料合併。

2．如檢驗結果拒絕檢驗假設，只能認為各總體率或總體構成比之間總的來說有差別，但不能說明它們彼此之間都有差別，或某兩者間有差別。

五、配對計數資料x²檢驗（x²testof paired comparison of enumeration data）

在計量資料方面，同一對象實驗前後差別或配對資料的比較與兩樣本均數比較方法有所不同；在計數資料方面亦如此。例如表20-16是28份咽喉塗抹標本，每份按同樣條件分別接種在甲、乙兩種白喉桿菌培養基中，觀察白喉桿菌生長情況，試比較兩種培養基的效果。

表20-16 兩種白喉桿菌培養基培養結果比較

甲培養基	乙培養基		合計
	+	-
+	11(a)	9(b)	20
-	1(c)	7(d)	8
合計	12	16	28

從表中資料可見有四種結果：（a）甲₊乙₊，（b）甲₊乙_-（c）甲_-乙₊,(d)甲_-乙_-；如果我們目的是比較兩種培養基的培養結果有無差異，則（a）、(d)兩種結果是一致的，對差異比較毫無意義，可以不計，我們只考慮結果不同的(b)和(c)，看其差異有無意義，可以應用以下簡易公式計算：

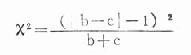公式（20.18）

檢驗步驟：

1．檢驗假設

H₀：π₁=π₂

H₁:π₁≠π₂

α=0.05

2．計算x²值

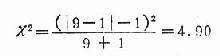
3．確定P值和分析 配對資料v=1，查附表20-1得知x20.05(1)=3.84,x2＞x0.05(1),P＜0.05,按α=0.05水準，拒絕H0，可以認為甲培養基的白喉桿菌生長效率較高。

如果b+c＞40，則可採用：

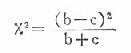公式（20.19）

此外還有兩種以上處理方法的比較，可參閱預防醫學專業的醫學統計方法有關章節。

附表20-1 x²界值表

v	P			V	P
	0.05	0.01	0.001		0.05	0.01	0.001
1	3.84	6.63	10.83	16	26.30	32.00	39.25
2	5.99	9.21	13.81	17	27.59	33.14	40.79
3	7.81	11.34	16.27	18	28.87	34.18	42.31
4	9.49	13.28	18.47	19	30.14	36.19	43.82
5	11.07	15.09	20.52	20	31.41	37.57	45.32
6	12.59	16.81	22.46	21	32.67	38.93	46.80
7	14.07	18.48	24.32	22	33.92	40.29	48.27
8	15.51	20.09	26.12	23	35.17	41.64	49.73
9	16.92	21.67	27.88	24	36.42	42.98	51.18
10	18.31	23.21	29.59	25	37.65	44.31	52.62
11	19.68	24.72	31.26	26	38.89	45.64	54.05
12	21.03	26.22	32.91	27	40.11	46.96	55.48
13	22.36	27.69	34.53	28	41.34	48.28	56.89
14	23.68	29.14	36.12	29	42.56	49.59	58.30
15	25.00	30.58	37.70	30	43.77	50.89	59.70

率的假設檢驗——正態近似法 | 秩和檢驗

關於「預防醫學/x2檢驗」的留言：	訂閱討論RSS
目前暫無留言
添加留言

更多醫學百科條目