生物化學與分子生物學/參考:別構機制的模式

跳轉到: 導航, 搜索

生物化學與分子生物學

酶
- 酶的作用特點
- 酶的分類和命名
- 酶的分子組成和化學結構
- 酶的作用機理
- 酶促反應的動力學
- 酶在體內存在的幾種主要形式
- 參考:別構機制的模式

生物化學與分子生物學目錄

別構機制的模式

為了解釋別構酶協同效應的機制並推導出動力學曲線的方程式，不少人曾提出過各種模式，各有優缺點，現在主要把Hill模式敘述如下：

Hill模式

在協同結合模式中最早的一種是Hill在1909年提出的，企圖解釋氧結合至血紅蛋白的S形飽和曲線，現稱為Hill模式，後來經Atkinson應用於別構酶反應，他設想在這個系統中，n分子的配體(S)能夠一步結合到酶上去：

即此反應的總解離常數(K's)由下式決定

K'S=［E］［S］n/［ESS］	(6-7)

而酶的飽和分數

YS=每分子酶蛋白上已結合的底物分子數/每分子酶蛋白上底物結合位點的總數	(6-8)

又因總的酶濃度［E0］=［E］+［ES0］

故　YS=［ESn］/［E0］=［ESn］/［ESn］+［E］	(6-9)

合併式6-7和式6-9，消去［ESn］，則

YS=［S］n/K'S+［S］n			(6-10)
YSK'S+YS［S］n=［S］n,
YSK'S=(1-Y)［S］n			(6-11)
Ys/1-Ys=［S］n/K'S			(6-11)
log	YS	=nlog［S］-logK'S	(6-13)
	1-YS

因此以

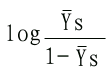對log［S］作圖的話，可得斜率為n，縱軸截距為-logK'S的直線(見下圖)。

因v=k0［ESu］,Vm=k0［E0］，故

=［ESu］／［E0］=v／vω	(6-14)

將式6-10代入式6-14，即得

［S］n/K'S+［S］n=v/Vm
Vm［S］n=K'Sv+v［S］n	(6-15)
(Vm-v)［S］n=K'Sv	(6-16)
v/Vm-v=［S］n/K'S	(6-17)
logv/Vm-v=nlog［S］-logK'S	(6-18)

式6-13或6-18即為Hill方程式，式6-18如以logv/Vm-v對log［S］作圖，也可得一直線(見下圖)。

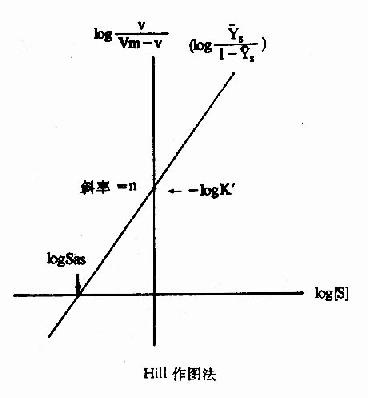
Hill作圖法

如v=Vm／2時，式6-19為log1=nlog［S］-logK'S=0(6-19)

此時的［S］即S0.5，故nlogS0.5=logK'5(6-20)式6-18所得的直線斜率為n，縱軸截距為-logk'S,而橫軸截距為logK'S/n，即log［S］0.5，但［S0.5］也可在已知logK'S後通過式6?0求取。

上節已述及，S0-5就相當於米曼氏動力學中的Km,當K0《k-1／k1時，可反映別構酶對底物的親和力，S0.5愈小，親和力愈大，而K's實際上已與親和力關係不大，因受到n的影響。故反映底物親和力的參數，已從非別構酶的Km一項移到別構酶的［S］一項，並且式6?0可看出K'S是隨［S］而改變的，不是一個常數。由於K'S的測定是假設V=(1/2)Vm或［S］=S0.5的條件下計算的，故有些作者用S0.5S，來代表別構酶的K'5，以免與Km混淆。

Hill作圖法的斜率n，稱為Hill係數，即前述的協同係數，一般可用nH或h代表。當nH=1時，式6-1變為V=Vm［S］/(K1+［S］)，即米曼氏方程式，表示無協同作用，此時K'或S0.5S，=S0-5=Km，至於nH＞1為正協同，nH＜1為負協同。

Hill模式比較簡單，式6-1或式6-10都是S形曲線方程式，但有不少缺點：(1)按理，Hill係數應等於酶分子中可能有結合底物的位點數，但因忽略了ESn-1,ESn-2…ES1等中間形式的酶底物複合體，根據Hill氏作圖計算出來的n值一般均低於真實的位點數。以別構蛋白 Hb為例，理論上每分子Hb可結合四分子氧，即n=4，但計算結果n=2.6～2.8。在負協同效應時，每分子酶也結合n個底物(n＞1)但計算結果卻是n＜1。故Hill係數已不能代表結合底物的位點數，而只能作為底物協同性的指標。(2)在S濃度過高(酶90%以上被S飽和)或過低(酶僅10%以下被S飽和)時，Hill線的斜率n常等於1，故當測定別構酶活力時，［S］的範圍較廣，得出的Hill線不是直線而是折線(見下圖)。(3)n分子的底物同時和酶作用，反應的級數為n+1，如n-4則為五級反應，這在動力學上是不可能的。但儘管如此，Hill作圖法仍不失是一個求取別構酶S0.5和鑒定協同類型及協同作用大小的常用方法。

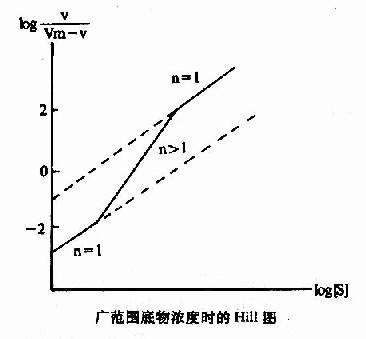
廣範圍底物濃度時的Hill圖