醫用化學/滴定分析概念
| 醫學電子書 >> 《醫用化學》 >> 滴定分析 >> 滴定分析概念 |
| 醫用化學 |
|
|
目錄 |
一、滴定分析的特點和方法
滴定分析是通過「滴定」來實現的一種分析方法。在滴定過程中,使用的已知準確的溶液稱為標準溶液,被滴定的溶液叫做試樣溶液。當標準溶液與被測組成的反應恰好完全時,即為反應的理論終點,稱為化學計量點附近發生的、容易觀察到的變化來確定。若反應本身無此種變化,就須藉助指示劑。指示劑所指示的反應終點稱為滴定終點。
滴定分析法是基於標準溶液與被測組分間發生化學反應時,它們的量之間存在一定的化學計量關係,利用標準溶液的濃度和所消耗的體積來計算被測物質含量的一種方法。根據分析時所利用的化學反應不同,滴定分析又分為酸鹼滴定法,氧化還原滴定法,配合滴定法和沉澱滴定法。
值得注意的是,並非所有的反應都可用於滴定分析,適合滴定分析的反應必須滿足以下條件:第一,該反應必須按一定的反應式進行,即必須具有確定的化學計量關係;第二,反應必須能夠定量地進行,通常要求達到99.9%以上;第三,必須有適當的方法確定反應的終點。此外要求反應能較快地進行。對於速度較慢的反應有時可通過加熱或加入催化劑來加速反應。
二、滴定分析的操作程序
(一)標準溶液的配製
1.直接配製法
直接稱取一定量的基準物質,溶解後轉入容量瓶中,稀釋定容。根據溶質的量和溶液的體積可計算出該溶液的準確濃度。
所謂基準物質是指那些能夠直接用來配製溶液的物質。它們必須符合下列條件:
(1)物質的組成應與化學式相符。若含結晶水,其結晶水的含量也應與化學式相符。
(2)試劑要純度高。一般含量在99.9%以上。
(3)試劑要穩定。如不易吸收空氣中的水分及二氧化碳,不易被空氣氧化等。
(4)有比較大的摩爾質量,以減少稱量所引起的相對誤差。
常用的基準物質有鄰酸氫鉀、草酸、碳酸鈉等。
2.間接配製法
由於大多數試劑不能滿足基準物質的條件,也就不能直接用來配製標準溶液。這時可先將它們配成近似所需濃度的溶液,再用下述方法標定其濃度,這種方法稱為間接配製法。
(二)標準溶液濃度的標定
標定是指用滴定方法確定溶液準確濃度的過程。可以用待標定溶液一定量的基準濃度,亦可以用待標定溶液和已知準確濃度的標準溶液進行相互滴定,比較出待測溶液的濃度。例如,欲標定鹽酸溶液的濃度,可稱取一定量的分析純碳酸鈉(基準物質)溶於水中,然後用此鹽酸溶液進行滴定:
2HCL+Na2CO3→2NaCL+H2O+CO2
當反應完全時,從用去此鹽酸溶液的體積和碳酸鈉的質量,即可求出鹽酸溶液的準確濃度。
(三)被測物質含量的測定
標準溶液的濃度確定後,即可對待測物質進行含量測定。例如,已標定的鹽酸溶液可以用來測定某些鹼性物質含量;已標定的氧化劑溶液可以用來測定某些還原性物質相對含量。
三、滴定分析的計算方法
(一)方向方法
滴定分析中的計算主要包括標準溶液濃度的計算和被測定物質含量的計算。標準溶液的濃度常用物質的量濃度表示。物質B的濃度即可用下式求得:
cB=nB/Vb (7-1)
或 cBVB=mB/MB(7-2)
在上面式子中,mb 為物質B的質量(g);MB 為物質B的摩爾質量(g˙mol-1);VB為物質B溶液的體積(L);cB即為物質B的量濃度(mol˙L-1)。
對於任一滴定反應:
aA+bB=dD+eE
若選取aA和bB作為基本單元,則有如下關係:
n(aA)=n(bB)(7-3)
上式表示:當達到化學計量點時,aA與bB的物質的量相等,即等物質的量規則。該規則是進行滴定分析計算的主要根據之一,由式(7-1)和式(7-3)得:
c(aA)˙V(A)=c(bB)˙V(B)
在實際工作中,為方便起見,常將A和B選作基本單元。
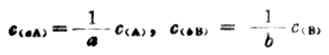
故式(7-4)又可寫成:
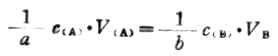
式(7-2)和(7-5)是滴定分析中兩個常用的計算式,下面通過實例介紹它們的應用。
例1 準確稱取基準物質K2Cr2O72.4530g,溶解後移入500ml容量瓶中,加水稀釋至刻度。求c(K2Cr2O7)和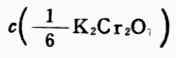 。
。
解:K2Cr2O7的摩爾質量為294.2g.mol-1
故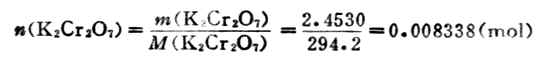
則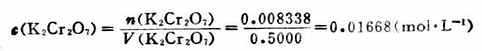
![]()
例2 稱取分析純Na2CO31.2738g,溶於水後稀釋成250mL,取該溶液25.00mL,用HCl溶液進行滴定,以甲基橙為指示劑。當達終點時,用去HCl溶液24.80mL,求此溶液的準確濃度。
解:滴定反應為
Na2CO3+2HCl→2NaCl+CO2+H2O
由式(7-5)得
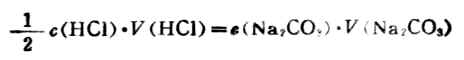
因為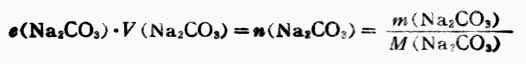
所以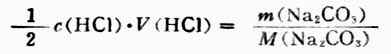
在上式中溶液的體積是以升為單位,若體積V指定以毫升為單位,則上式可化為
則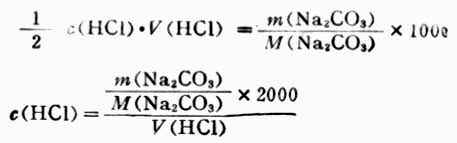
在25.00mL Na2CO3溶液中Na2CO3的質量為:
所以 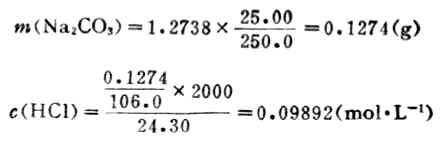
例3 稱取草酸0.1670g溶於適量的水中,用0.1000mol.L-1的NaOH標準溶液滴定,用去23.46mL,求樣品中H2C2O4.2H2O的質量百分數。
解:滴定反應為
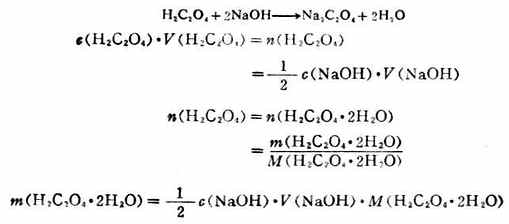
則草酸的質量百分數:
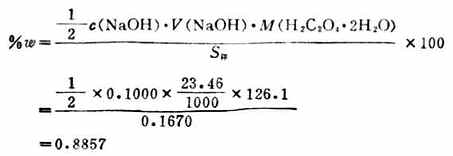
(二)有效數字和計算規則
有效數字是指實際上能測量到的數值,在該數值中只有最後一位是可疑數字,其餘的均為可靠數字。它的實際意義在於有效數字能反映出測量時的準確程度。例如,用最小刻度為0.1cm的直尺量出某物體的長度為11.23cm,顯然這個數值的前3位數是準確的,而最後一位數字就不是那麼可靠,因為它是測試者估計出來的,這個物體的長度可能是11.24cm,亦可能是11.22cm,測量的結果有±0.01cm的誤差。我們把這個數值的前面3位可靠數字和最後一位可疑數字稱為有效數字。這個數值就是四位有效數字。
在確定有效數字位數時,特別需要指出的是數字「0」來表示實際測量結果時,它便是有效數字。例如,分析天平稱得的物體質量為7.1560g,滴定時滴定管讀數為20.05mL,這兩個數值中的「0」都是有效數字。在0.006g中的「0」只起到定位作用,不是有效數字。
在計算中常會遇到下列兩種情況:一是化學計量關係中的分數和倍數,這些數不是測量所得,它們的有效數字位數可視為無限多位;另一種情況是關於pH、pK和lgK等對數值,其有效數字的位數僅取決於小數部分的位數,因為整數部分只與該真數中的10的方次有關。例如,pH=13.15為兩位有效數字,整數部分13不是有效數字。若將其表示成[H+]=7.1×10-14,就可以看出13的作用僅是確定了[H+]在10-14數量級上,其數學意義與確定小數點位置的「0」相同。
在滴定分析中,實驗數據的記錄只應保留一位可疑數字,結果的計算和數據處理均應按有效數字的計算規則進行。
在進行加減運算時,有效數字取捨以小數點後位數最少的數值為準。例如,0.0231、24.57和1.16832三個數相加,24.57的數值小數點後位數最少,故其他數值也應取小數點後兩位,其結果是
0.02+24.57+1.17=25.76
在乘除運算中,應以有效數字最少的為準。例如,0.0231、24.57和1.16832三個數相乘,0.0231的有效數字最少,只有3位,故其他數字也只取3位。運算的結果也保留3位有效數字:
0.0231×24.6×1.17=0.665
在對數運算中,所取對數的位數應與真數的有效數字位數相同。例如,lg9.6的真數有兩位有效數字,則對數應為0.98,不應該是0.982或0.9823。又如[H+]為3.0×10-2mol.L-1時,PH應為1.52。
正確運用有效數字規則進行運算,不但能夠反映出計算結果的可信程度,而且能大大簡化計算過程。在滴定分析中一般常採用四位有效數字。
四、滴定分析的誤差
(一)誤差及其來源
在滴定分析中,分析結果的準確度常用誤差來表示。誤差是測量值與真實值之間的差異,它反映出分析結果與真實值間的符合程度。努力減少測量誤差,提高分析結果的準確性是定量分析中的一項重要課題。
滴定分析中最常見的誤差有系統誤差和偶然誤差。
1.系統誤差
系統誤差是由某些必然的或經常的原因造成的。其來源有方法誤差,儀器、試劑誤差及操作誤差等。系統誤差對分析結果的影響有一定的規律性,在重複測量時誤差的大小常常比較接近,並且會反覆出現。與理論值相比,實驗值要麼都提高,要麼都偏低。系統誤差常用作空白試驗和對照實驗的方法消除或克服。
在不加試樣的情況下,按照樣品分析步驟和條件進行分析試驗稱為空白試驗,所得結果稱為空白值。從試樣測定結果中扣除空白值,便可以消除因試劑、蒸餾水及實驗儀器等因素引起的系統誤差。
將組分含量已知的標準樣品和待測樣品在相同條件下進行分析測定。用標準樣品的測定值與其真實值的差值來校正其他測量結果,這種方法稱為對照試驗。
除此之外,還可以通過校準儀器來消除儀器誤差,通過制訂正確的操作規程克服操作誤差。
2.偶然誤差
偶然誤差是由一系列微小變化的偶然原因造成的。例如,稱量同一物體時,室溫或濕度如有微小變動都會引起偶然誤差,使得稱量結果不一致。這種誤差大小不定,時正時負,往往找不出確定的原因,因些很難控制、校正和測定它。但偶然誤差符合統計規律,表現為正負誤差出現的機會相等,小誤差出現的機會多而大誤差出現的機會少。因此,在消除了系統誤差的前提下,可以通過增加測定次數取平均值的辦法克服偶然誤差。
(二)誤差與準確度
準確度指實驗測定值(X)與真實值(T)之間的符合程度,常用誤差的大小來衡量。誤差的絕對誤差和相對誤差。絕對誤差指測定值與真實值之間的差值,用「E」來表示。相對誤差指的是絕對誤差占真實值的百分率,用「%RE」表示。即
絕對誤差:E=X-T
相對誤差:(%)RE=E/T×100
誤差越小,表示實驗結果與真實值越接近,測定的準確度也越高。而與絕對誤差相比,相對誤差更能反映出實驗結果的準確程度。因此在滴定分析中一般多採用相對誤差來表示測量的準確度。
(三)偏差與精密度
在實際工作中真實值往往是不知道的,此時便不好用誤差來評價分析結果,通常用相同條件下多次測定結果的平均值(X) 來代替真實值,用偏差來衡量所得結果的精密試。
精密度指多次重複測定的結果相互接近的程度,是保證準確度的前提。偏差是指各次測定的結果和平均值之間的差值。偏差越小,精密度越高。
偏差分為絕對偏差(d)、相對偏差(Rd)、平均偏差(d)和相對平均偏差 (Rd),它們的表達式為:
絕對偏差![]()
相對偏差![]()
平均偏差![]()
相對平均偏差![]()
式中d1,d2…dn為第1,2…n次測量結果的偏差,X為單次測定值,x為測定平均值。
對於一般的滴定分析來講,因測定次數不多,故常用相對平均偏差來表示實驗的精密度。
| 關於「醫用化學/滴定分析概念」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |