預防醫學/集中趨勢指標
| 醫學電子書 >> 《預防醫學》 >> 計量數據分析(一) >> 集中趨勢指標 |
| 預防醫學 |
|
|
平均數是統計中應用最廣泛、最重要的一個指標體系。常用的有算術均數、幾何均數、中位數三個指標。它們用於描述一組同質計量資料的集中趨勢或反映一組觀察值的平均水平。
目錄 |
一、算術均數（arithmetic mean）
簡稱對數（mean）。習慣上以表示樣本均數，以希臘字母μ表示總體均數。均數適用於對稱分布，特別是正態或近似常態分佈的計量資料，其計算方法有：
（一）直接法
當樣本的觀察值個數不多時，將各觀察值X1，X2，……，Xn相加再除以觀察值的個數n（樣本含量）即得均數。其公式為：
公式（18.1）
式中，希臘字母Σ（讀作sigma）是求和的符號。
例18.1 某地11名20歲健康男大學生身高（cm）分別為174.9,173.1, 171.8,179.0,173.9,172.7,166.2,170.8,171.8,172.1,168.5。試計算其均數。
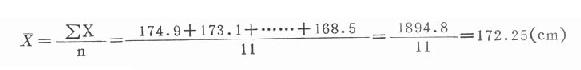
（二）加權法
當觀察值個數較多時，可先將各觀察值分組歸納成頻數表，用加權法求均數。其計算步驟如例18.2。
例18.2 某地1993年隨機測量了該地110名20歲健康男大學生的身高(cm)，資料如下，試計算其均數。
| 173.9 | 173.9 | 166.9 | 179.5 | 171.2 | 167.8 | 177.1 | 174.7 | 173.8 | 182.5 |
| 173.6 | 165.8 | 168.7 | 173.6 | 173.7 | 177.8 | 180.3 | 173.1 | 173.0 | 172.6 |
| 173.6 | 175.3 | 178.4 | 181.5 | 170.5 | 176.4 | 170.8 | 171.8 | 180.7 | 170.7 |
| 173.8 | 164.4 | 170.0 | 175.0 | 177.7 | 171.4 | 162.9 | 179.0 | 174.9 | 178.3 |
| 174.5 | 174.3 | 170.4 | 173.2 | 174.5 | 173.7 | 173.4 | 173.9 | 172.9 | 177.9 |
| 168.3 | 175.0 | 172.1 | 166.9 | 172.7 | 172.2 | 168.0 | 172.7 | 172.3 | 175.2 |
| 171.9 | 168.6 | 167.6 | 169.1 | 166.8 | 172.0 | 168.4 | 166.2 | 172.8 | 166.1 |
| 173.5 | 168.6 | 172.4 | 175.7 | 178.8 | 169.1 | 175.5 | 170.3 | 171.7 | 164.6 |
| 171.2 | 169.1 | 170.7 | 173.6 | 167.2 | 170.7 | 174.7 | 171.8 | 167.3 | 174.8 |
| 168.5 | 178.7 | 177.3 | 165.9 | 174.0 | 170.2 | 169.5 | 172.1 | 178.2 | 170.9 |
| 171.3 | 176.1 | 169.7 | 177.9 | 171.1 | 179.3 | 183.5 | 168.5 | 175.5 | 175.9 |
1.編製頻數表
（1）求全距（range）：找出觀察值中的最大值（183.5）和最小值（162.9），它們的差值即全距，常用R表示。本例R=20.6。
（2）定組距和組段：相鄰兩組的最小值之差稱組距，常用i表示，各組距可相等，也可不相等，一般用等距。常取全距的1/10，取整作組距。本例全距的1/10為2.06，取整為2，用等距共劃分11個組段。第一組段應包括資料中最小值，最末組段應包括最大值，一般要求組段的起點為較整齊的數。本例第一組段的起點（即下限）取162，其止點（即上限）為第二組段的起點即164，然後每一組距（本例為2）就成為一組段，最末組段應同時寫出下限和上限，本例為182～184。
（3）列表劃記：按上述的組段序列排列製表，用正字劃記法將例18.2中的數據歸納到各組段中，最後清點出頻數得頻數表，表18-1中的第（2）、（3）欄。
表18-1 110名20歲健康男大學生身高(cm)的頻數分布
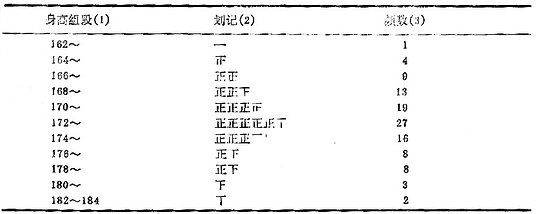
由頻數表的頻數分布可看出兩個重要特徵：集中趨勢和離散趨勢。集中趨勢即頻數分布向中央部分集中；離散趨勢即頻數分布由中央到兩側逐漸減少。頻數分布可為①對稱分布或近似常態分佈，即集中位置在正中，兩側頻數分布大致對稱，如表18-1；②偏態分布，即集中位置偏向一側，頻數分布不對稱，若集中位置偏向數值小的一側，為正偏態分布；若集中位置偏向數值大的一側，為負偏態分布。不同類型的分布，應採用相應描述指標和統計分析方法。
2．計算公式
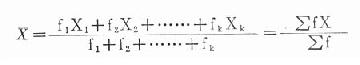公式（18.2）
式中，k為組段數；f1,f2,……,fk分別為各組段的頻數；X1，X2，……，Xk分別為各組段的組中值，組中值為本組段的下限與相鄰較大組段的下限相加除以2，如「162-」組段的組中值X1=（162+164）/2=163，余仿此。
3．列計算表（表18-2）計算均數
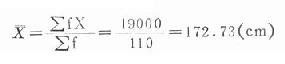
110名20歲健康男大學生身主的均數為172.73(cm)。
二、幾何均數（geometric mean）
用G表示。常用於等比級數資料和對數對稱分布，尤其是對數常態分佈的計量資料。對數常態分佈即原始數據呈偏態分布，經對數變換後（用原始數據的對數值lgX代替X）服從常態分佈。其計算方法有：
表18-2 110名20歲健康男大學生身高（cm）均數的計算表（加權法）
| 身高級段（1） | 組中值X（2） | 頻數f（3） | FX(4)=(2)×(3) |
| 162～ | 163 | 1 | 163 |
| 164～ | 165 | 4 | 660 |
| 166～ | 167 | 9 | 1503 |
| 168～ | 169 | 13 | 2197 |
| 170～ | 171 | 19 | 3249 |
| 172～ | 173 | 27 | 4671 |
| 174～ | 175 | 16 | 2800 |
| 176～ | 177 | 8 | 1416 |
| 178～ | 179 | 8 | 1432 |
| 180～ | 181 | 3 | 543 |
| 182～184 | 183 | 2 | 366 |
| 合計 | 110(Σf) | 19000(ΣfX) |
（一）直接法
當觀察值個數n不多時，直接將n個觀察值（X1，X2，……Xn）的乘積開n次方。其計算公式為：
公式（18.3）
其對數形式：
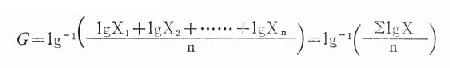公式（18.4）
例18.3 設有6份血清的抗體效價為1：10，1:20，1:40，1:80，1:80，1:160。求其平均效價。
本例可將各抗體效價的倒數代入公式（18.4），求平均效價數的倒數。
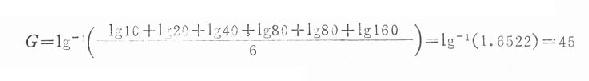
該6份血清的平均抗體效價為1:45。
（二）加權法
當觀察值個數n較多時，先將觀察值分組歸納成頻數表，再用公式（18.5）計算。
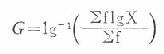公式（18.5）
式中，X為各組段的效價或滴度的倒數（等比級數資料時）或各組段的組中值（對數常態分佈資料時）；f 為各組段所對應頻數。
例18.430名麻疹易感兒童接種麻疹疫苗一個月後，血凝抑制抗體滴度如表18-3第（1）、（2）欄，試求其平均抗體滴度。
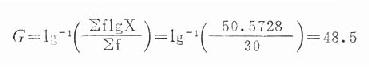
30名麻疹易感兒童免疫後的平均血凝抑制滴度為1:48.5。
三、中位數（median）
中位數是一組按大小順序排列的觀察值中位次居中的數值，用M表示。它常用於描述偏態分布資料的集中趨勢。中位數不受個別特小或特大觀察值的影響，特別是分布末端無確定數據不能求均數和幾何均數，但可求中位數。計算方法有：
表18-3 平均抗體滴度計算表
| 抗體滴度（1） | 人數f（2） | 滴度倒數X（3） | lgX（4） | flgX(5)=（2）×（4） |
| 1:8 | 2 | 8 | 0.9031 | 1.8062 |
| 1:16 | 6 | 16 | 1.2041 | 7.2246 |
| 1:32 | 5 | 32 | 1.5051 | 7.5255 |
| 1:64 | 10 | 64 | 1.8062 | 18.0620 |
| 1:128 | 4 | 128 | 2.1072 | 8.4288 |
| 1:256 | 2 | 256 | 2.4082 | 4.8164 |
| 1:512 | 1 | 512 | 2.7093 | 2.7093 |
| 合計 | 30（Σf） | 50.5728(ΣflgX) | ||
（一）直接法
當n較小時，可直接由原始數據求中位數。先將觀察值由小到大按順序排列，再按公式（18.6）或公式（18.7）計算。
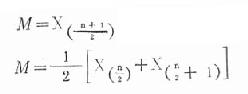公式（18.6）
(n為偶數時) 公式（18.7）
式中，n 為觀察值的總個數，X的右下標(n+1/2)、（n/2）、和（n/2+1）為有序數列中觀察值的位次，X(n+1/2)、X（n/2）和X（n/2+1）為相應位次上的觀察值。
例18.5 某病患者9名，其發病的潛伏期順序為2，3，3，3，4，5，6，9，16天，求中位數。
本例n=9，為奇數，按公式（18.6）計算
若上例在第20天又發現一例患者，則患者數增為10名，n為偶數，按公式（18.7）計算
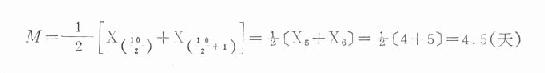
（二）頻數表法
當n較大時，先將觀察值分組歸納成頻數表，再按組段由小到大計算累計頻數和累計頻率。如表18-4中的（3）、（4）兩欄，然後按公式（18.8）計算。
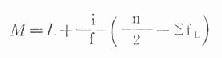公式（18.8）
式中，L為中位數（即累計頻率為50%）所在組段的下限；i為該組段的組距；f為該組段的頻數；ΣfL為小於L的各組段的累計頻數；n為總例數。
例18.6 求表18-4中數據的中位數
表18-4 164名食物中毒潛伏期的中位數和百分位數*計算表
| 潛伏期（小時 ）（1） | 人數f（2） | 累計頻數（Σf）（3） | 累計頻率（%）（4） |
| 0～ | 25 | 25 | 15.2 |
| 12～ | 58 | 83 | 50.6 |
| 24～ | 40 | 123 | 75.0 |
| 36～ | 23 | 146 | 89.0 |
| 48～ | 12 | 158 | 96.3 |
| 60～ | 5 | 163 | 99.4 |
| 72～84 | 1 | 164 | 100.0 |
- 百分位數的意義與計算見後面的［附］.
由表18-4可見，50%在「12～」組段內，則L=12，i=12,f=58,ΣfL=25,n=164,按式（18.8）計算
M=L+i/f(n/2-ΣfL)=12+12/58(164/2-25)=23.8(小時)
［附］百分位數：百分位數是一個位置指標，用Px表示。當P1，P2，……，P98，P99確定後，一個由小到大的有序數列即被分為100等份，各含1%的觀察值。百分位數常用於描述一組偏態分布資料在某百分位置上的水平及確定偏態分布資料的醫學正常值範圍。第50百分位數（P50）也就是中位數，所以，中位數也是一個特定的百分位數。計算百分位數用公式（18.9）
Px＝L＋i/fx（n.x%-ΣfL）公式（18.9）
式中，L、i、fx分別為Px所在組段的下限、組距和頻數；ΣfL為小於L的各級段的累計頻數。
例18.7 求表18-4中數據的P95。
求P95時，x=95，即累計頻率為95%所在組段。本例為「48～」組段，則L=48，i=12，fx=12,ΣfL=146,n=164,代入公式、（18.9）
P95=48+12/12（164×95%-146）=57.8（小時）
 計量數據分析(一) | 離散趨勢指標  |
| 關於「預防醫學/集中趨勢指標」的留言： |  訂閱討論RSS
|
|
目前暫無留言 | |
| 添加留言 | |