預防醫學/離散趨勢指標
| 醫學電子書 >> 《預防醫學》 >> 計量數據分析(一) >> 離散趨勢指標 |
| 預防醫學 |
|
|
計量資料的頻數分布有集中趨勢和離散趨勢兩個主要特徵，只有把兩者結合起來，才能全面地認識事物，通過例18.8可進一步說明這一問題。
例18.8 有3組同齡男孩體重（kg）如下，其平均體重x都是30（kg），試分析其離散趨勢。
| 甲組 | 26 | 28 | 30 | 32 | 34 |
| 乙組 | 24 | 27 | 30 | 33 | 36 |
| 丙組 | 26 | 29 | 30 | 31 | 34 |
雖然三組資料的均數相等，即集中趨勢相同，但各組內數據參差不齊的程度（變異度）不同，也就是說三組的離散趨勢不同。
描述一組同質計量資料離散趨勢的常用指標有全、四分位數間距方差和標準差，其中方差和標準差最常用。
目錄 |
一、全距（range）
亦稱極差，用R表示。全距是一組觀察值中最大值與最小值之差，用於反映個體變異範圍的大小。全距大，說明變異度大；反之，說明變異度小。如例18.8中乙組全距為12(kg)，比甲、丙兩組8（kg）大，表明乙組變異度大。全距適用於任何分布的計量資料（末端無確切數值者除外）。
用全距來表達變異度的大小，簡單明了，故曾廣為使用。但它不能反映組內所有數據的變異度，如上述甲、丙兩組變異度的差異就反映不出來；其更大的缺點是易受個別特大或特小數值的影響，往往樣本越大，全距亦會越大。
二、四分位數間距（quartile interval）
四分位數間距是上四分位數Qu（即P75）與下四位數QL（即P25）之差，其間包括了全部觀察值的一半，用Q表示。它和極差類似，數值越大，說明變異越大；反之，說明變異越小。四分位數間距比極差穩定，但仍未考慮到每個觀察值的變異度。它適用於偏態分布資料，特別是分布末端無確定數據不能計算全距、方差和標準差的資料。
例18.9 求表18-4中數據的四分位數間距。
QL=P25=12+12/58（164×25%-25）=15.3(小時)
Qu=P75=24+12/40(164×75%-83)=36.0(小時)
Q=Qu-QL=P75-P25=20.7（小時）
三、方差（variance）和標準差（standard deviation）
為了克服極差的缺點，需全面地考慮組內每個觀察值的離散情況。因為組內每一觀察值（亦稱變數值）與總體均數的距離大小都會影響總體的變異度，故有人提出以各變數值離均差（X-μ）的平方和除以變數值的總個數N，來反映變異度大小，稱為總體方差，用σ2示之。
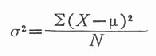公式(18.10)
由式可見，各個離均差平方後，原來的度量單位變成了平方單位。為了用原單位表示而將總體方差開方，稱為總體標準差。
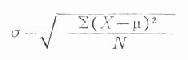公式（18.11）
以上是總體方差和標準差。實際工作中經常得到的是樣本資料，μ是未知的，只能用樣本均數x來代替μ，用樣本含量n代替N，按公式（18.11）算得的標準差常比σ小，美國統計學家W.S.Gosset提出用n-1代替n，求得樣本標準差s，即
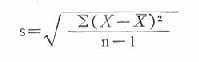公式（18.12）
式中的n-1，在統計學上稱為自由度（degree of freedom）
數學上可以證明離均差平方和Σ（X-x）2=ΣX2-（ΣX）2/n，故公式（18.2）可演變為：
直接法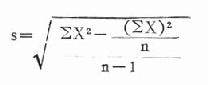
公式（18.13）
加權法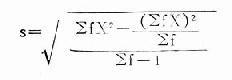
公式（18.14）
方差與標準差適用於對稱分布，特別是正態或近似常態分佈資料。
例18.10 試分別計算例18.8中組男孩體重資料的標準差。
甲組：n=5，ΣX=26=28+30+32+34=150
ΣX2=262+282+302+322+342=4540
按式（18.13）
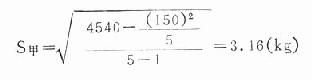
乙組：n=5，ΣX=150，ΣX2=4590
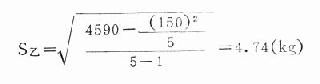
丙組：n=5,ΣX=150,ΣX2=4534
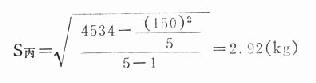
以上計算表明：S丙＜S甲＜S乙亦即乙組的變數度最大，甲組次之，丙組最小。
例18.11 求表18-2中110名20歲健康男大學生身高的標準差。
由表18-2，已知Σf=110，ΣfX=19000，再用第（2）欄乘第（4）欄後相加得ΣfX2。如本例，ΣfX2=163×163+165×660+……+183×366=3283646代入式（18.14）
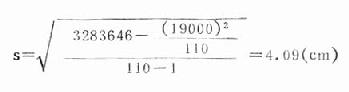
四、標準差的應用
（一）表示觀察值的變異程度（或離散程度）
1．在兩組（或幾組）資料均數相近、度量單位相同的條件下，標準差大，表示觀察值的變異度大，即各觀察值離均數較遠，均數的代表性較差；反之，表示各觀察值多集中在均數周圍，均數的代表性較好。
2．若比較度量單位不同或均數相差懸殊的兩組（或幾組）觀察值的變異度時，需計算變異係數（coefficient ofvariation用CV表示）進行比較，其計算公式為：
CV= s/x×100% 公式（18.15） 公式(18.15)
式中s為樣本標準差，x為樣本均數。
例18.12 某地調查20歲男大學生110名，其身高均數為172.73(cm),標準差為4.09(cm)；其體重均數為55.04(kg)，標準差為4.10(kg)，欲比較兩者變異度何者為大，宜先計算變異係數再比較。
身高CV=4.09/172.73×100%=2.37%
體重CV=4.10/55.04×100%=7.45%
由此可見，該地20名男大學生體重的變異度大於身高的變異度，說明身高這個指標比較穩定。
（二）結合均數描述常態分佈的特徵和估計醫學正常值範圍，詳見第三節。
（三）結合樣本含量n計算標準誤，詳見第十九章。
 集中趨勢指標 | 常態分佈和醫學正常值範圍的估計  |
| 關於「預防醫學/離散趨勢指標」的留言： |  訂閱討論RSS
|
|
目前暫無留言 | |
| 添加留言 | |