藥理學/連續恆速給藥

跳轉到: 導航, 搜索

藥理學

藥物代謝動力學
- 藥物消除動力學
  - 零級消除動力學
  - 一級消除動力學
  - 連續恆速給藥
  - 一級藥動學指標間的相互關係
  - 房室模型

臨床治療常需連續給藥以維持有效血藥濃度。在一級動力學藥物中，開始恆速給藥時藥物吸收快於藥物消除，體內藥物蓄積。按計算約需5個t_1/2達到血藥穩態濃度（C_ss）(圖3-8)，此時給藥速度（RA）與消除速度（RE）相等。

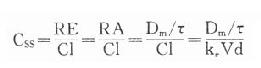
(τ為給藥間隔時間)可見C_ss隨給藥速度(RA=D_m/τ)快慢而升降，到達C_ss時間不因給藥速度加快而提前，它取決於藥物的k_e或t_1/2。據此，可以用藥物的k_eVd或Cl計算給藥速度以達到所需的有效藥物濃度。靜脈恆速滴注時血藥濃度可以平穩地到達C_ss。分次給藥雖然平均血藥濃度上升與靜脈滴注相同，但實際上血藥濃度上下波動（圖3-8）。分藥間隔時間越長波動越大，其峰值濃度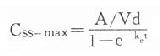　

，谷值濃度 C_{ss- min}=C_{ss- max}e 。如果實際C_ss過高或過低，可以按已達到的C_ss與需要達到的C_ss比值調整給藥速度，即C_ss（已達到的）/C_ss（需要的）=RA（現用的）/RA（將調整的）

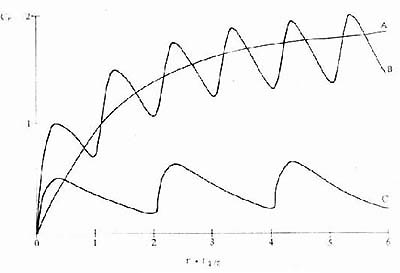
圖3-8 連續恆速給藥時的時量曲線
約經5個半衰期血藥濃度達到穩態。給藥間隔越短，
血藥濃度波動越小。給藥劑量越大，血藥濃度越高

A.靜脈滴注，D_m/t_1/2B.肌肉注射，D_m/t_1/2
C.肌肉注射，1/2D_m/2t_1/2。D_m維持劑量

但從調整劑量時開始需再經過5個t1/2方能達到需要的Css。

在病情危重需要立即達到有效血藥濃度時，可於開始給藥時採用負荷劑量(loading dose,D1),因為

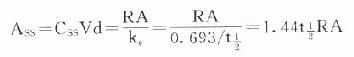
A_ss就是負荷劑量。可將第一個t_1/2內靜脈滴注量的1.44倍在靜脈滴注開始時推注入靜脈即可立即達到並維持C_ss。在分次恆速給藥達到C_ss時，體內A_ss是維持劑量(maintenance dose, D_m)與體內上一劑量殘留藥物的和，即

當給藥間隔時間τ=t1_/2時，

即每隔一個t_1/2給藥一次時採用首劑加倍劑量的D1可使血藥濃度迅速達到Css。

理想的給藥方案應該是使CSS- max略小於最小中毒血漿濃度（MTC）而CSS- min略大於最小有效血漿濃度（MEC），即血藥濃度波動於MTC與MEC之間治療窗，這一Dm可按下列公式計算：

Dm=（MTC － MEC）Vd

負荷劑量計演算法與上同，即D1=ASS=1.44t1/2 RA=1.44t1/2　Dm/τ，τ為給藥間隔時間。τ可按一級消除動力學公式推算得

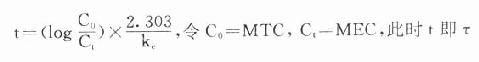
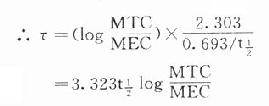
因此可以根據藥物的MTC及MEC利用這些公式計算出D₁，D_m及τ。注意此時 τ≠t_1/2，D₁≠2D_m（圖3-9）。

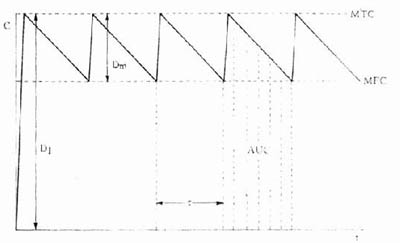
圖3-9 負荷劑量、維持劑量、給藥間隔與血藥濃度關係
D_m維持劑量所形成的C D₁負荷劑量所形成的C

在零級動力學藥物中，體內藥量超過機體最大消除能力。如果連續恆速給藥，RA>RE，體內藥量蓄積，血藥濃度將無限增高。停藥後消除時間也較長，超過5個t1/2。因為t1/2=0.5C0/K，達到C0越高t1/2越長。

臨床用藥可根據藥動學參數如Vd、Cl、ke、t1/2及AUC等按以上各公式計算劑量及設計給藥方案以達到並維持有效血藥濃度。除了少數t1/2特長或特短的藥物，或零級動力學藥物外，一般可採用每一個半衰期給於半個有效量(half dose at half life interval)並將首次劑量加倍是有效、安全、快速的給藥方法。

有些藥在體內轉化為活性產物則需注意此活性產物的藥動學，如果活性產物的消除是藥物消除的限速步驟的話，則應按該產物的藥動學參數計算劑量及設計給藥方案。