生理學/血流量和血流速度
| 醫學電子書 >> 《生理學》 >> 血液循環 >> 血管生理 >> 血流量、血流阻力和血壓 >> 血流量和血流速度 |
| 生理學 |
|
|
單位時間內流過血管某一截面的血量稱為血流量,也稱容積速度,其單位通常以ml/min或L/min來表示。血液中的一個質點在血管內移動的線速度,稱為血流速度。血液在血管流動時,其血流速度與血流量成正比,與血管的截面成反比。
1.泊肅葉(Poiseuilli)定律泊肅葉研究了液體在管道系統內流動的規律,指出單位時間內液體的流量(Q)與管道兩端的壓力差P1-P2以及管道半徑r的4次成正比,與管道的長度L成反比。這些關係可用下式表示:
Q=K(r4/L)(P1-P2)
這一等式中的K為常數。後來的研究證明它與液體的粘滯度η有關。因此泊肅葉定律又可寫為
Q=π(P1-P2)r4/8ηL
2.層流和湍流血液在血管內流動的方式可分為層流和湍流兩類。在層流的情況下,液體每個質點的流動方向都一致,與血管的長軸平行;但各質點的流速不相同,在血管軸心處流速最快,越靠近管壁,流速越慢。因此可以設想血管內的血液由無數層同軸的圓柱面構成,在同一層的液體質點流速相同,由軸心向管壁,各層液體的流速依次遞減,如圖4-18所示。圖中的箭頭指示血流的方向,箭的長度表示流速,在血管的縱剖面上各箭頭的連線形成一拋物線。泊肅葉定律適用於層流的情況。當血液的流速加快到一定程度後,會發生湍流。此時血液中各個質點的流動方向不再一致,出現旋渦。在湍流的情況下,泊肅葉定律不再適用,血流量不是與血管兩端的壓力差成正比,而是與壓力差的平方根成正比。關於湍流的形成條件,Reynolds提出一個經驗公式:
Re=VDσ/η
式中的V為血液在血管內的平均流速(單位為cm/s),D為管腔直徑(單位為cm),σ為血液密度(單位為g/cm3),η為血液沾滯度(單位為泊),Re為Reynolds數,沒有單位。一般當Re數超過2000時,就可發生湍流。由上式可知,在血流速度快,血管口徑大,血液粘滯度低的情況下,容易產生湍流。
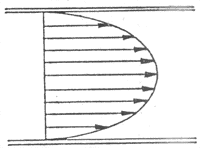
圖4-18 層流情況下各層血液的流速
| 關於「生理學/血流量和血流速度」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |