預防醫學/u檢驗和t檢驗
| 醫學電子書 >> 《預防醫學》 >> 計量數據分析(二) >> u檢驗和t檢驗 |
| 預防醫學 |
|
|
u檢驗和t檢驗可用於樣本均數與總體均數的比較以及兩樣本均數的比較。理論上要求樣本來自常態分佈總體。但在實用時，只要樣本例數n較大，或n小但總體標準差σ已知時，就可應用u檢驗；n小且總體標準差σ未知時，可應用t檢驗，但要求樣本來自常態分佈總體。兩樣本均數比較時還要求兩總體方差相等。
目錄 |
一、樣本均數與總體均數比較
比較的目的是推斷樣本所代表的未知總體均數μ與已知總體均數μ0有無差別。通常把理論值、標準值或經大量調查所得的穩定值作為μ0。根據樣本例數n大小和總體標準差σ是否已知選用u檢驗或t 檢驗。
（一）u檢驗 用於σ已知或σ未知但n足夠大［用樣本標準差s作為σ的估計值，代入式（19.6）］時。
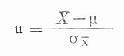公式（19.6）
以算得的統計量u，按表19-3所示關係作判斷。
表19-3 u值、P值與統計結論
| α | ｜t｜值 | P值 | 統計結論 |
| 0.05雙側 單側 |
＜1.96 ＜1.645 |
＞0.05 | 不拒絕H0，差別無統計學意義 |
| 0.05雙側 單側 |
≥1.96 ≥1.645 |
≤0.05 | 拒絕H0，接受H1，差別有統計學意義 |
| 0.01雙側 單側 |
≥2.58 ≥2.33 |
≤0.01 | 拒絕H0，接受H1，差別有高度統計學意義 |
例19.3根據大量調查，已知健康成年男子脈搏均數為72次/分，標準差為6.0次/分。某醫生在山區隨機抽查25名健康成年男子，求得其脈搏均數為74.2次/分，能否據此認為山區成年男子的脈搏高於一般？
據題意，可把大量調查所得的均數72次/分與標準差6.0次/分看作為總體均數μ0和總體標準差σ，樣本均數x為74.2次/分，樣本例數n為25。
H0: μ=μ0
H1: μ＞μ0
α=0.05(單側檢驗)
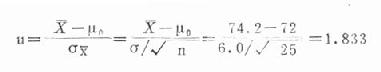
算得的統計量u=1.833＞1.645,P＜0.05,按α=0.05檢驗水準拒絕H0，可認為該山區健康成年男子的脈搏高於一般。
（二）t檢驗 用於σ未知且n較小時。
公式（19.7）
以算得的統計量t，按表19-4所示關係作判斷。
表19-4 ｜t｜值、P值與統計結論
| α | ｜t｜值 | P值 | 統計結論 |
| 0.05 | ＜t0.05(v) | ＜0.05 | 不拒絕H0，差別無統計學意義 |
| 0.05 | ≥t0.05(v) | ≤0.05 | 拒絕H0，接受H1，差別有統計學意義 |
| 0.01 | ≥t0.01(v) | ≤0.01 | 拒絕H0，接受H1，差別有高度統計學意義 |
例19.4 若例19.3中總體標準差σ未知，但樣本標準差已求出，s=6.5次/分，餘數據同例19.3。
據題意，與例19.3不同之處在於σ未知，可用t檢驗。
H0: μ=μ0
H1: μ＞μ0
α=0.05(單側檢驗)
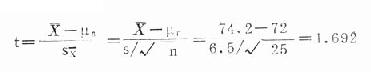
本例自由度v=25-1=24，查t界值表（單側）（附表19-1）得t0.05(24)=1.711。算得的統計量t=1.692＜1.711,P＞0.05，按α=0.05檢驗水準不拒絕H0，尚不能認為該山區成年男子的脈搏高於一般。
二、配對資料的比較
在醫學研究中，常用配對設計。配對設計主要有四種情況：①同一受試對象處理前後的數據；②同一受試對象兩個部位的數據；③同一樣品用兩種方法（儀器等）檢驗的結果；④配對的兩個受試對象分別接受兩種處理後的數據。情況①的目的是推斷其處理有無作用；情況②、③、④的目的是推斷兩種處理（方法等）的結果有無差別。
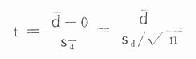公式（19.8）
式中，0為差數年總體均數，因為假設處理前後或兩法無差別，則其差數的均數應為0，d為一組成對數據之差d（簡稱差數）的均數，其計算公式同式（18.1）；Sd為差數均數的標準誤，sd為差數年的標準差，計算公式同式（18.3）；n為對子數。
因計算的統計量是t，按表19-4所示關係作判斷。
例19.5 應用某藥治療9例高血壓病人，治療前後舒張壓如表19-5，試問用藥前後舒張壓有無變化？
表19-5 高血壓病人用某藥治療前後的舒張壓（kPa）
| 病人編號 | 治療前 | 治療後 | 差數d | D2 |
| 1 | 12.8 | 11.7 | 1.0 | 1.21 |
| 2 | 13.1 | 13.1 | 0.0 | 0.00 |
| 3 | 14.9 | 14.4 | 0.5 | 0.25 |
| 4 | 14.4 | 13.6 | 0.8 | 0.64 |
| 5 | 13.6 | 13.1 | 0.5 | 0.25 |
| 6 | 13.1 | 13.3 | -0.2 | 0.04 |
| 7 | 13.3 | 12.8 | 0.5 | 0.25 |
| 8 | 14.1 | 13.6 | 0.5 | 0.25 |
| 9 | 13.3 | 12.3 | 1.0 | 1.00 |
| 合計 | 4.7 | 3.89 |
H0：該藥治療前後的舒張壓無變化，即μd=0
H1:該藥治療前後的舒張壓有變化，即μd≠0
α=0.05
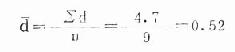
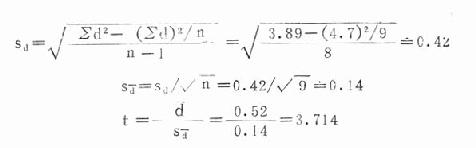
自由度v=n-1=8，查t界值表得t0.05(8)=2.306,t0。01（8）=3.355，本例t=3.714＞t0.01(8),P＜0.01,按α=0.05檢驗水準拒絕H0，接受H1，可認為治療前後舒張壓有變化，即該藥有降壓作用。
三、完全隨機設計的兩樣本均數的比較
亦稱成組比較。目的是推斷兩樣本各自代表的總體均數μ1與μ2是否相等。根據樣本含量n的大小，分u檢驗與t檢驗。
（一）u檢驗 可用於兩樣本含量n1、n2、均足夠大時，如均大於50或100。
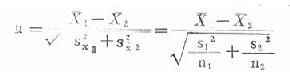公式（19.9）
算得的統計量為u 值，按表19-3所示關係作出判斷。
例19.6某地抽樣調查了部分健康成人紅細胞數，其中男性360人，均數為4.660×1012/L，標準差為0.575×1012/L；女性255人，均數為4.178×1012/L，標準差為0.291×1012/L，試問該地男、女紅細胞數的均數有無差別？
H0: μ=μ0
H1: μ≠μ0
α=0.05
今x1=4.660×1012/L,s1=0.575×1012/L,n1=360；
x2=4.1781012/L,s2=0。2911012/L，n2=255.
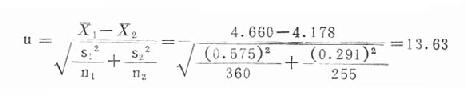
算得的u=13.63＞2.58,P＜0.01,按 α=0.05檢驗水準拒絕H0，接受H1，可認為該地男女紅細胞數的均數不同，男性高於女性。
（二）t檢驗 可用於兩樣本含量n1、n2較小時，且要求兩總體方差相等，即方差齊（homoscedasticity）。若被檢驗的兩樣本方差相差較大且差別有統計學意義則需用t'檢驗。
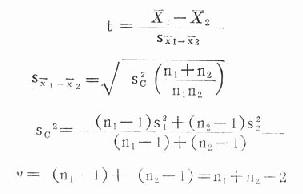
公式（19.10）
公式（19.11）
公式（19.12）
式中sx1－x2，為兩樣本均數之差的標準誤，s2c為合併估計方差（combined estimate variance）。算得的統計量為t，按表19-4所示關係作出判斷。
例19.7某醫生統廣西瑤族和侗族正常婦女骨盆X線測量資料各50例。骨盆入口前後徑：瑤族的均數為12.002(cm)，標準差0.948(cm)，侗族相應的為11.456(cm)和1.215(cm)。問兩族婦女的骨盆入口前後徑是否有差別？
H0: μ1=μ2
H1: μ1≠μ2
α=0.05
已知n1=n2=50,x1=12.002(cm),s1=0.948(cm)；
x2=11.456(cm),s2=1.215(cm).
本例自由度v=n1+n2-2=98,查t界值表［表內自由度一欄無98，可用內插法（從略）或用v =100估計］。T0.05(100)=1.948,t0.01(100)=2.626,今t=2.505＞t0.05(1000,P＜0.05,按α=0.05檢驗水準拒絕H0，接受H1，可認為廣西瑤族和侗族婦女骨盆入口前後徑不同，前者大於後者。
四、完全隨機設計的兩樣本幾何均數比較
醫學上有些資料為等比資料或常態分佈資料，宜用幾何均數表示其平均水平。比較兩樣本幾何均數的目的是推斷它們分別代表的總體幾何均數是否相等。此種情況下，應先把原始數據X進行對數變換，用變換後的數據代入式（19.10）、(19.11)、(19.12)計算t值。
例19.8 將20名鉤端螺旋體病人的血清隨機分為兩組，分別用標準株或水生株作凝溶試驗，測得稀釋倍數如下，問兩組的平均效價有無差別？
X1：標準株（11人）100，200，400，400，400，400，800，1600，1600，1600，3200
X2：水生珠（9人）100，100，100，200，200，200，200，400，400
H0: μ1=μ2
H1: μ1≠μ2
α=0.05
將兩組數據分別取對數，以對數作為新變數X1和X2。
X1：2.000,2.301,2.602,2.602,2.602,2.602,2.903,3.204,3.204,3.204,3.505
X2:2.000,2.000,2.000,2.301,2.301,2.301,2.301,2.602,2.602
用變換後的數據計算 x1，s12；x2，s22再代入式（19.10）、(19.11)、(19.12)計算t值。
x1=2.794,s12=0.2043；x2=2.268,s22=0.0554
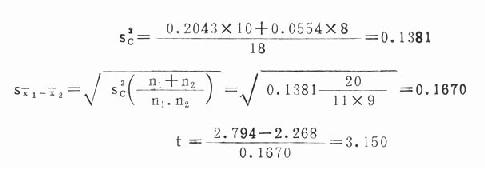
自由度v=11+9-2=18，查t界值表得t0.01(18)=2.878,今t=3.150＞2.878,P＜0.01，按α=0.05檢驗水準拒絕H0，接受H1，可認為兩組平均效價不同，標準株高於水生株。
 假設檢驗的基本步驟 | 方差分析  |
| 關於「預防醫學/u檢驗和t檢驗」的留言： |  訂閱討論RSS
|
|
目前暫無留言 | |
| 添加留言 | |