預防醫學/回歸分析
| 醫學電子書 >> 《預防醫學》 >> 相關回歸分析 >> 回歸分析 |
| 預防醫學 |
|
|
|
醫學上,不少孌量間雖存在一定關係,但這種關係不象函數關係那樣十分確定。例如正常人的血壓隨年齡而增高,但這只是總的趨勢,有些高齡人的血壓卻不一定偏高;一群正常人按年齡和血壓兩個變數在坐標上的方位點,並非集中在一條上升直線上,而是圍繞著一條有代表性的直線上升。
直線回歸分析的任務在於找出兩個變數有依存關係的直線方程,以確定一條最接近於各實測點的直線,使各實測點與該線的縱向距離的平方和為最小。這個方程稱為直線回歸方程,據此方程描繪的直線就是回歸直線。
(一)直線回歸方程式(linear regression equation)的計算
直線回歸方程的通式為:
=a+bX 公式(22.3)
式中Y為自由變數X推算因變數Y的估計值,a為回歸直線在Y軸上的截距,即X=0時的Y值;b為樣本回歸係數(regression coefficient),即回歸直線的斜率(slope或稱坡度),表示當X變動一個單位時,Y平均變動b個單位。如果已知a與b,用以代入公式(22.3),即可求得直線回歸方程。求a和b的公式分別為:
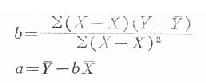
公式(22.4)
公式(22.5)
對樣本中兩個變數分析,不但可作相關分析,還可進一步作直線回歸分析。仍以表22-1為示範,該例經過直線相關分析,r=0.6097,兩變數間有直線關係,從相關係數計算時,已求得:
Σ(X-x)(Y-Y)=41.2000
Σ(X-x)2=677.4194
而Y=ΣY/n=99.2/31=3.2000
x=ΣY/n=534/31=17.2258
代入公式(22.4)
b=41.2000/677.4194=0.0608
代入公式(22.5)
a=3.2000-0.0608×17.2258=2.1527
代入公式(22.3)
=2.1527+0.0608X
(二)樣本回歸係數的假設檢驗
樣本回歸係數也有抽樣誤差問題,故需對b作假設檢驗,以評估b是否可能從回歸係數為零(即β=0)的總體中隨機抽得的。
檢驗步驟:
H0:β=0 即b是由β=0的總體中隨機抽樣的樣本回歸係數。
H1:β≠0
α=0.05
t檢驗:檢驗公式為
tb=|b|/sb公式(22.6)
式中sb是回歸係數的標準誤,計算公式為
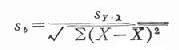 公式(22.7)
公式(22.7)
式中sy.x為各觀察值Y距回歸直線(Y)的標準差,是當X的影響被扣除後Y方面的變異指標。可用以下公式計算:
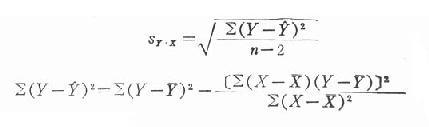
公式(22.8)
公式(22.9)
本例上述已算得
Σ(X-x)2=677.4194
Σ(Y-Y)2=6.7400
Σ(X-x)(Y-Y)=41.2000
分別代入公式(22.9),(22.8),(22.7)和(22.6)得
Σ(Y-Y)2=6.7400-41.20002/677.4194=4.2343
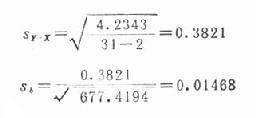
tb=0.0608/0.01468=4.1417
分析評價 本例自由度v=31-2=29,查t值表,t0.01(29)=2.756,P<0.01,按α=0.05檢驗水準,拒絕無效假設,可以認為待產婦24小時尿中雌三醇含量與初生兒體重之間存在直線回歸關係。
(三)描繪回歸直線
根據以上求得回歸方程Y=2.1527+0.0608x,可以在自變數X的實測範圍內(本例為7~27)任取X1和X2兩值代入上式求得在圖22-2中的P1(X1,Y1)和P2(X2,Y2)兩坐標點,將兩點連結為一直線,就屬該方程的回歸直線。作圖要注意的是P1、P2兩點最好距離遠些,繪出的直線在坐標上誤差就小些。
| 關於「預防醫學/回歸分析」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |