預防醫學/小樣本病例隨訪資料統計分析
| 醫學電子書 >> 《預防醫學》 >> 病例隨訪 >> 小樣本病例隨訪資料統計分析 |
| 預防醫學 |
|
|
|
隨訪病例較少時，可按下法求不同時期的生存率（或緩解率）及其統計學意義分析。
一、資料統計方法和曲線描繪分析
例23.3某單位用甲、乙兩法治療何杰金病。甲法治療15例中已複發9例；乙法治療14例，有4例複發。兩組隨訪情況如表23-3。
先以甲療法為例說明不同隨訪時期的緩解率及其標準誤。演算結果如表23-4。
表23-4 甲、乙兩法治療何杰金病隨訪天數
| 甲療法 | 乙療法 | ||
| 已複發者 | 尚未複發者 | 已複發者 | 尚未複發者 |
| 141 | 1446+ | 505 | 615+ |
| 364 | 836+ | 296 | 570+ |
| 950 | 498+ | 1375 | 1205+ |
| 570 | 173+ | 688 | 1726+ |
| 312 | 1540+ | 1190+ | |
| 570 | 836+ | 822+ | |
| 173 | 1408+ | ||
| 401 | 1493+ | ||
| 86 | 1645+ | ||
| 1570+ | |||
尚未複發者隨訪天數後加「+」號，表明緩解天數至少多於隨訪天數
表23-4 甲療法治療何杰金病不同時期緩解率計算
| 病序（1） | 隨訪天數n（2） | 複發例數r（3） | 期初病例數R（4） | 複發機率qx(5) | 緩解機率px(6) | 累計緩解機率np0(7) | 標準誤snp0(8) |
| 1 | 86 | 1 | 15 | 0.0667 | 0.9333 | 0.933 | 0.064 |
| 2 | 141 | 1 | 14 | 0.0714 | 0.9286 | 0.867 | 0.088 |
| 3 | 173 | 1 | 13 | 0.0769 | 0.9231 | 0.800 | 0.103 |
| 4 | 173 | … | 12 | 0.0000 | 1.0000 | 0.800 | - |
| 5 | 312 | 1 | 11 | 0.0909 | 0.9091 | 0.727 | 0.117 |
| 6 | 364 | 1 | 10 | 0.1000 | 0.9000 | 0.654 | 0.126 |
| 7 | 401 | 1 | 9 | 0.1111 | 0.8889 | 0.581 | 0.131 |
| 8 | 498+ | … | 8 | 0.0000 | 1.0000 | 0.581 | — |
| 9 | 570 570 |
2 | 7 | 0.2857 | 0.7143 | 0.415 | 0.136 |
| 10 | |||||||
| 11 | 836 836 |
… | 5 | 0.0000 | 1.0000 | 0.415 | — |
| 12 | |||||||
| 13 | 950 | 1 | 3 | 0.3333 | 0.6667 | 0.277 | 0.145 |
| 14 | 1446+ | … | 2 | 0.0000 | 1.0000 | 0.277 | — |
| 15 | 1540+ | … | 1 | 0.0000 | 1.0000 | 0.277 | - |
1．按隨訪天數從小到大依次排列，如遇複發者天數和未複發者隨訪天數相同時，以複發者排在前面。
2．填寫不同隨訪天數的複發例數及期初病例數如表23-4的（3）、（4）欄。
3．求出不同隨訪天數的複發機率qx（複發例數÷期安病例數）和緩解機率px(1-qx)如（5）、（6）欄。
4．根據公式（23.6）求出累計緩解機率np0如(7)欄。
5．按下式求不同時點累計緩解率的標準誤。
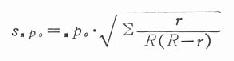公式（23.8）
本例173天時點累計緩解率的標準誤：
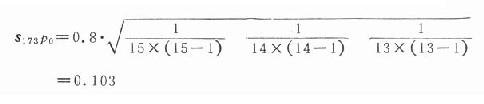
同法可以求得乙療法的累計緩解率及其標準誤，學者試自演算求解。
6．緩解率曲線描繪以橫軸為隨訪天數（n），縱軸為累計緩解率（np0）,將兩療法的演算結果各點的坐標準確標出，然後將各點向右連成與橫軸平行的階梯形，得出兩組緩解曲線如圖23-1。可以看出乙療法累計緩解率水平始終在甲法之上。
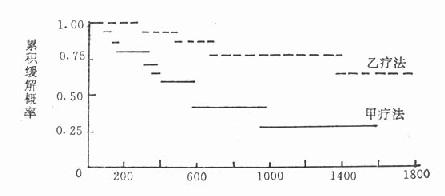
圖23-1 甲、乙療法累計緩解率的比較
二、兩療法差異的統計學意義分析
如果要分析兩療法差異有無統計學意義，可用時序檢驗法（log rank test）。假定兩組療法效果相同，求各時點預期複發數，再進一步作x2檢驗。演算如表23-5。
表23-5按檢驗假設算得甲、乙兩組的預期複發數（即理論值）和實際數，分別為：
A甲=9，T甲=5.138；A乙=4，T乙=7.817
代入x2檢驗公式
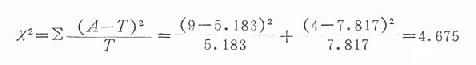
查x2值表，x20.05(1)=3.84,今x2＞4.675,P＜0.05,表明兩法累計緩解率曲線的差別有統計學意義。
表23-5 甲、乙兩療法預期複發數計算表
| 療法分組（1） | 觀察天數（2） | 複發例數 | 期初病例數 | 預期複發數 | |||||
| 甲組（3） | 乙組（4） | 合計（5）=（3）+（4） | 甲組（6） | 乙組（7） | 合計（8）=（6）+（7） | 甲組（9）=（5）（6）/（8） | 乙組（10）=（5）（7）/（8） | ||
| 甲 | 86 | 1 | 1 | 15 | 14 | 29 | 0.517 | 0.483 | |
| 甲 | 141 | 1 | 1 | 14 | 14 | 28 | 0.500 | 0.500 | |
| 甲 | 173 | 1 | 1 | 13 | 14 | 27 | 0.481 | 0.519 | |
| 甲 | 173＋ | … | 12 | 14 | 26 | … | … | ||
| 乙 | 296 | 1 | 1 | 11 | 14 | 25 | 0.440 | 0.560 | |
| 甲 | 812 | 1 | 1 | 11 | 13 | 24 | 0.458 | 0.542 | |
| 甲 | 364 | 1 | 1 | 10 | 13 | 23 | 0.435 | 0.565 | |
| 甲 | 401 | 1 | 1 | 9 | 13 | 22 | 0.409 | 0.591 | |
| 甲 | 498＋ | … | 8 | 13 | 21 | … | … | ||
| 乙 | 505 | 1 | 1 | 7 | 13 | 20 | 0.350 | 0.650 | |
| 甲 甲 |
570 ＞570 |
1 ＞2 1 |
1 ＞ 1 |
7 | 12 | 19 | 0.737 | 1.263 | |
| 乙 | 570＋ | … | 5 | 12 | 17 | … | |||
| 乙 | 615＋ | … | 5 | 11 | 16 | … | |||
| 乙 | 688 | 1 | 1 | 5 | 10 | 15 | 0.333 | 0.667 | |
| 乙 | 822＋ | … | 5 | 9 | 14 | … | … | ||
| 甲 | 836＋ ＞ 836+ |
… … ＞ … |
5 | 8 | 13 | … | … | ||
| 甲 | |||||||||
| 甲 | 950 | 1 | 1 | 3 | 8 | 11 | 0.273 | 0.727 | |
| 乙 | 1190＋ | … | 2 | 8 | 10 | … | … | ||
| 乙 | 1205＋ | … | 2 | 7 | 9 | … | … | ||
| 乙 | 1375 | 1 | 1 | 2 | 6 | 8 | 0.250 | 0.750 | |
| 乙 | 1408＋ | … | 2 | 5 | 7 | … | … | ||
| 甲 | 1446＋ | … | 2 | 4 | 6 | … | … | ||
| 乙 | 1493＋ | … | 1 | 4 | 5 | … | … | ||
| 甲 | 1540＋ | … | 1 | 3 | 4 | … | … | ||
| 乙 | 1570＋ | … | 0 | 3 | 3 | … | … | ||
| 乙 | 1645＋ | … | 0 | 2 | 2 | … | … | ||
| 乙 | 1726＋ | … | 0 | 1 | 1 | … | … | ||
| 總和 | (A)9 | (A)4 | 13 | 15 | 14 | 29 | (T)5.183 | (T)7.817 | |
 生存率的壽命表法 | 人群健康狀況評價  |
| 關於「預防醫學/小樣本病例隨訪資料統計分析」的留言： |  訂閱討論RSS
|
|
目前暫無留言 | |
| 添加留言 | |