型別理論
| A+醫學百科 >> 型別理論 |
在最廣泛的層面上,類型論是關注把實體分類到叫做類型的搜集中的數學和邏輯分支。在這種意義上,它與類型的形上學概念有關。現代類型論在部分上是響應羅素悖論而發明的,並在伯特蘭·羅素和阿弗烈·諾夫·懷海德的《數學原理》中起到重要作用。
在計算機科學分支中的程式語言理論中,類型論提供了設計分析和研究類型系統的形式基礎。實際上,很多計算機科學家使用術語「類型論」來稱呼對程式語言的類型語言的形式研究,儘管有些人把它限制於對更加抽象的形式化如有類型lambda演算的研究。
目錄 |
簡單的類型論
下面的系統是Mendelson的(1997: 289-93)ST。量化的域被劃分成上升的類型層次,帶有所有的個體都被指派了一個類型。量化的變數確立範圍只在一個類型上;所以底層邏輯是一階邏輯。ST是"簡單的"(相對於《數學原理》中的類型論)主要是因為任何關係的域和陪域的所有成員都必須是同一個類型的。
有一個最低的類型,它的個體沒有成員並且是次最低類型的成員。最低類型的個體對應於特定集合論中的基本元素(urelement)。每個類型都有一個更高的類型,類似於在皮亞諾算術中後繼者。ST對是否有極大類型保持沉默,形成超限數個類型沒有困難。這些因素,和回應於皮亞諾公理,使它方便和習慣於指派自然數到每個類型,開始於0給最低類型。這個類型論不要求自然數的先決定義。
ST的特有符號是加右上角標的變數和中綴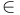 。在任何給定的公式中,無角標的變數都有相同的類型,而有角標的變數(x')取值於更高的類型上。ST的原子公式與兩種形式,x = y(同一性)和
。在任何給定的公式中,無角標的變數都有相同的類型,而有角標的變數(x')取值於更高的類型上。ST的原子公式與兩種形式,x = y(同一性)和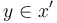 。中綴符號
。中綴符號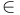 暗示了預想的釋義,集合成員關係。
暗示了預想的釋義,集合成員關係。
出現在同一性定義和外延和概括公理中所有變數都取值於連貫的兩個類型之上。一個"低層"類型和另一個"高層"類型。取值於高層類型上的變數加角標;而取值於低層類型的變數不加。ST的一階公式化排除在類型上的量化。所以每對連續的類型都要求它自己的外延和概括公理,如果「外延」和「概括」公理採用公理模式的方式取值於類型上就是可能的。
同一性定義:![x=y \Leftrightarrow \forall z' [x \in z' \leftrightarrow y \in z']](/images/math/1/e/d/1edfdc25ac365c7dd30c385313dddd1c.png) 。
。
外延公理|外延公理模式:![\forall x[x \in y' \leftrightarrow x \in z'] \Rightarrow y'=z'](/images/math/b/c/e/bce5faf12bc296167f884c5ccd0222c7.png) 。
。
設Φ(x)表示包含自由變數x的任何一階公式。
概括公理模式:![\exists z' \forall x[x \in z' \leftrightarrow \Phi(x)]](/images/math/9/2/b/92b43c542fe526fe5a8c5639471e75e9.png) 。
。
備註:相同類型的元素的任何搜集都可以形成更高類型的一個對象。概括公理有關於Φ(x)也有關於類型。
無窮公理|無窮公理。存在著在最低層類型的個體之上的非空二元關係R,它是反自反的、傳遞的和強連接的(![\forall x ,y [xRy \lor yRx]](/images/math/3/0/9/309426a86688b0a7f55e0d3b2587afcb.png) )。
)。
備註:無窮公理是ST的唯一真正的,並且本質上完全是數學的公理。R也是一個嚴格全序,帶有同一的域和陪域。如果0被指派給最低層類型(依次1是對(雙元素集合,單元素集合),2是有序對),R的類型是3。這個公理強迫一個無窮集合的存在,因為只有R的(陪)域是無窮的時候它才可以被滿足。如果關係以有序對的方式定義,這個公理要求有序對的先決定義;ST接受Kuratowski的定義。文獻沒有給出ZFC和其他集合論的無窮公理(存在歸納集合)不能結合於ST的理由。
ST披露了類型論可以制定得何其類似於公理化集合論。而ST更加精緻的本體論,根源於現在所謂的「集合的迭代構想」,導致了遠比有著更簡單的本體論的常規集合論如ZFC簡單得多的公理(模式)。公理化集合論起步於類型論,但是它的公理、本體論和術語不同於上面所述ST系統,還包括新基礎和Scott-Potter集合論。
參見
進一步閱讀
- Andrews, Peter B., 2002. An Introduction to Mathematical Logic and Type Theory: To Truth Through Proof, 2nd ed. Kluwer Academic Publishers.
- Cardelli, Luca, 1997, "Type Systems," in Allen B. Tucker, ed., The Computer Science and Engineering Handbook. CRC Press: 2208-2236.
- Mendelson, Elliot, 1997. Introduction to Mathematical Logic, 4th ed. Chapman & Hall.
- Pierce, Benjamin, 2002. Types and Programming Languages. MIT Press. ISBN 0-262-16209-1)
- Thompson, Simon, 1991. Type Theory and Functional Programming. Addison-Wesley. ISBN 0-201-41667-0.
- Winskel, Glynn, 1993. The Formal Semantics of Programming Languages, An Introduction. MIT Press. ISBN 0-262-23169-7.
外部連結
- Stanford Encyclopedia of Philosophy: Type Theory" -- by Thierry Coquand.
- National Institute of Standards and Technology: Abstract data type
- A summary paper on the formal basis of ADTs, relationship to category theory, and list of good references. Pages 3-4 appear relevant. Reference number [6] looks good, but it may not be available online.
- Constable, Robert L., 2002, "Naïve Computational Type Theory," in H. Schwichtenberg and R. Steinbruggen (eds.), Proof and System-Reliability: 213-259.
- The Nuprl Book: "Introduction to Type Theory."
參考來源
| 關於「型別理論」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |