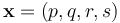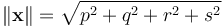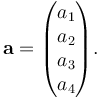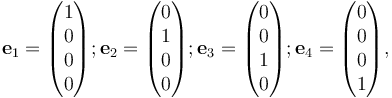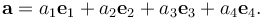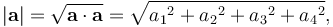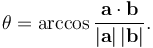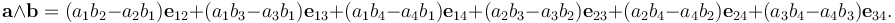四維

在2013年5月11日 (六) 12:43所做的修訂版本 (檢視原始碼) 行医 (對話 | 貢獻) (以内容''''四维'''，古代医书多用作四脏的代称。 分类:中医'创建新页面) ←上一版本		在2014年10月4日 (六) 23:14所做的修訂版本 (檢視原始碼) 行医 (對話 | 貢獻) 下一版本→
第1行：		第1行：
-	''' 四 维'''， 古代医书 多用作四 脏 的代称。	+	{{NoteTA|G1=Math
-	[[ 分 类:中 医]]	+	}}
		+
		+	{{Redirect2|四-{}-维|国之四-{}-维“礼义廉耻”|四维八德}}
		+	[[File:8-cell-simple.gif|thumb|200px|从三维投影看，一个在四维空间中绕一个平面旋转的[[四维超正方体]]。
		+
		+	在物理学和数学中，一个n个数的[[向量|序列]]可以被理解为一个''n''维[[欧几里得空间|空间]]中的[[坐标系|位置]]。当''n''=4时 ， 所有这样的位置的集合就叫做''四维空间''。这种空间与我们熟悉并在其中居住的三维空间不同，因为它 多 一个维数。这个额外的维数既可以理解成时间，也可以[[直接理解]]为空间的第'''四维'''，即'''第四空间维数'''。
		+
		+	== 作为时间的第四维数 ==
		+
		+	{{Main|时空}}
		+
		+	当人们说到“四维空间”时，经常指的都是关于时间的概念。在这种情况下，四维空间可以理解为三维空间附加一条时间轴。这种空间叫做闵可夫斯基时空或“(3 + 1)-空间”<ref name=Møller>
		+	{{cite book
		+	|author=C Møller
		+	|title=The Theory of Relativity
		+	|year= 1952
		+	|page=p. 93
		+	|url=http://books.google.com/books?id=Qu9SAAAAMAAJ&dq=intitle:the+intitle:theory+intitle:of+intitle:relativity+inauthor:moller&lr=&as_brr=0
		+	|publisher=Clarendon Press
		+	|location=Oxford UK
		+	|isbn=0198512562}}
		+	</ref>。这也是爱因斯坦在他的广义相对论和狭义相对论中提及的四维时空概念。
		+
		+	== 作为空间的第四维数 ==
		+
		+	第四维数可以 用 空间的方式理解，即一个有四个空间性维数的空间（“纯空间性”的四维空间），或者说有四个两两正交的运动方向的空间。这种空间就是数学家们用来研究四维几何物体的空间，与爱因斯坦提出的时间 作 为第 四 维数 的 理论不同。关于这一点，[[考克]]斯特曾写道：
		+
		+	{{Quote|把时间作为第四维数带来的好处即使有的话也是微不足道的。实际上，H. G. 威尔在《时间机器》中发展的这种十分吸引人的观点导致了J. W. 杜恩（《时间实验》）等作者对相对论的非常错误的理解。闵可夫斯基的时空几何是不符合欧几里得体系的，所以也就与当前的研究没有关系。- [[哈罗德·斯科特·麦克唐纳·考克斯特|H. S. M. 考克斯特]], ''Regular Polytopes''<ref>Coxeter, H. S. M. (1973). ''Regular Polytopes'', Dover Publications, Inc., p.&nbsp;119.</ref>}}
		+
		+	从数学方面讲，普通三维空间集合的四维等价物是[[欧几里得空间|欧几里得四维空间]]，一个四维欧几里得[[范数|赋范]][[赋范向量空间|向量空间]]。一个向量的“长度”
		+
		+	: <math> \mathbf{x} = (p, q, r, s) </math>
		+
		+	以标准基底表示就是
		+
		+	: <math> \| \mathbf{x} \| = \sqrt{p^{2} + q^{2} + r^{2} + s^{2}} </math>
		+
		+	也就是勾股定理向四维空间进行的很自然的类比。这就让两个向量之间的夹角很容易定义了（参见欧几里得空间）。
		+
		+	=== 正交性 ===
		+
		+	在我们熟悉的三维空间里，有三对主要方向：上下（高度），南北（纬度），东西（经度）。这三对方向两两正交，也就是说，它们两两成直角。从数学方面讲，它们在三条不同的坐标轴''x''、''y''、''z''上。计算机图形学中讲的深度缓冲指的就是这条''z''轴，在计算机的二维屏幕上 代 表深度。
		+
		+	纯空间性的四维空间另有一对垂直于其他三个主要方向的主要方向。这一对方向处在另一条同时垂直于''x''、''y''、''z''轴的坐标轴上，通常 称 作''w''轴。对这两个方向的命名，人们的看法不一。一些现行的命名有'''安娜'''/'''卡塔'''，'''斯皮希图'''/'''斯帕提图'''，'''维因'''/'''[[维奥]]'''，和'''宇普西龙'''/'''德尔塔'''。这些额外的方向处于（实际上是垂直于）我们所能观察到的三维世界中的方向之外 。
		+
		+	{| style="margin: 0 auto;" | [[File:Hypercubeorder.svg|220px|]] ||&nbsp;&nbsp;&nbsp;|| [[File:Hypercubecubes.svg|300px|]] ||&nbsp;&nbsp;&nbsp;|| [[File:Hypercubestar.svg|240px|]] |}
		+
		+	=== 向量 ===
		+
		+	{{expert}}
		+	[[File:Dice analogy- 1 to 5 dimensions.svg|thumb|right|400px|从一维到五维物体的演示。]]
		+	{{Main|向量}}
		+
		+	纯空间性四维空间可以以向量的形式理解。一个四维向量同样由'''方向'''和'''长度'''（又叫做'''模'''）组成，它可以认为是对从一个点到另一个点向某个方向移动一定的长度的这个过程的描述。零向量是一个长度为零的特殊向量，也就是描述“不移动”这个过程的向量。
		+
		+	==== 向量运算 ====
		+
		+	数学上四维空间可以简单理解为有四个坐标轴的空间，即在普通坐标系中需要4个参数来描述其中一点的坐标。 假设一个描述四维空间中一个点的向量为'''a'''，有
		+
		+	: <math>\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \end{pmatrix}.</math>
		+
		+	上式也可以写成由4个基底(如'''e'''<sub>1</sub>, '''e'''<sub>2</sub>, '''e'''<sub>3</sub>, '''e'''<sub>4</sub>)表示的形式，则
		+
		+	:<math>\mathbf{e}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}; \mathbf{e}_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}; \mathbf{e}_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}; \mathbf{e}_4 = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}, </math>
		+
		+	所以'''a'''可化为
		+
		+	: <math> \mathbf{a} = a_1\mathbf{e}_1 + a_2\mathbf{e}_2 + a_3\mathbf{e}_3 + a_4\mathbf{e}_4.</math>
		+
		+	四维向量的[[向量的加法|加法]]，[[向量的减法|减法]]和向量比例和空间向量的一致。空间向量中的数量积（或称为向量的“内积”、点乘）也被推广到四维向量中，如
		+
		+	: <math>\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 + a_4 b_4.</math>
		+
		+	下式可以用于计算一个四维向量的长度
		+
		+	:<math> \left| \mathbf{a} \right| = \sqrt{\mathbf{a} \cdot \mathbf{a} }  = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2 + {a_4}^2},</math>
		+
		+	而两个向量的夹角可由下式定义或计算
		+
		+	:<math> \theta = \arccos{\frac{\mathbf{a} \cdot \mathbf{b}}{\left|\mathbf{a}\right| \left|\mathbf{b}\right|}}.</math>
		+
		+	向量积（或称为向量的“外积”、叉乘）是一个常数，而空间向量的外代数定义为
		+
		+	: <math>\mathbf{a} \wedge \mathbf{b} = (a_1b_2 - a_2b_1)\mathbf{e}_{12} + (a_1b_3 - a_3b_1)\mathbf{e}_{13} + (a_1b_4 - a_4b_1)\mathbf{e}_{14} + (a_2b_3 - a_3b_2)\mathbf{e}_{23} + (a_2b_4 - a_4b_2)\mathbf{e}_{24} + (a_3b_4 - a_4b_3)\mathbf{e}_{34}.</math>
		+
		+	这是双矢量的求值，以基底('''e'''<sub>12</sub>, '''e'''<sub>13</sub>, '''e'''<sub>14</sub>, '''e'''<sub>23</sub>, '''e'''<sub>24</sub>, '''e'''<sub>34</sub>)在四维空间中的双矢构成了[[六维]]线性空间，它们可以被用来在四个方向产生旋转。
		+
		+	==== 向量操作 ====
		+
		+	通过改变一个四维向量的长度而不改变它的方向，我们可以对一个向量进行'''伸缩变换|伸缩'''。这可以被想象成沿着原向量的方向伸长或缩短一段长度。一个长度为负数的向量与和它方向相反、长度相等的正数的向量互为相反向量。这可以想象成面沿着原向量的方向倒着走。
		+
		+	如果沿着两个首尾相接的向量运动，那么描述这种运动的直接结果的向量就叫做这两个向量的向量和。例如，如果一个人从点A开始沿某一向量运动到点B，又从点B开始沿另一个向量运动到点C，那么这两个向量的和向量就是从点A径直到点C的向量。
		+
		+	==== 向量组合 ====
		+
		+	{{Main|线性组合}}
		+
		+	给定一组四维向量，我们可以对它们进行任意的伸缩和求和操作来得到新的四维向量。以这种方式得到的所有的四维向量的集合就叫做这一组向量的[[线性组合|组合]]。这种组合可以认为是一个点通过沿着一组向量中的某些向量移动所能达到的所有位置的集合。
		+
		+	给定几何图形X和向量集合S，如果从几何图形X内的一个点出发，沿着向量集合S的线性组合中的向量运动，能够到达X内所有其它的点，那么我们就说这个向量集合S可以'''张'''出几何图形X。
		+
		+	==== 向量基底 ====
		+
		+	{{Main|基底}}
		+
		+	能够张出一个几何图形X的最小向量集合叫做''X''的一组基底。不是所有的向量集合都是基底，因为它们可能含有赘余的向量。如果一个向量能通过集合中其他向量经过伸缩、求和而得到，那么这个向量就是赘余的。例如，如果一个集合中有两个平行的向量，那么它们中的一个可以被移除而 X 中的所有点仍然可以达到，因为能通过那个被移除的向量达到的点一定可以通过那个与它平行的向量达到。或者，如果一个向量是其他两个的和，那么它也完全可以被移除。零向量总是赘余的，因为它并不能让一个人达到任意一个除他已经能够达到的点之外的点。
		+
		+	==== 维数 ====
		+
		+	通过把任意一个可以张出几何图形''X''的向量集合中的所有赘余向量移除，我们可以过的一组''X''的基底。选定的初始向量集合不同，获得的能张出 X 的基底也可能不同；但是，可以证明所有这些基底中都含有相同数量的向量。这个数量就叫做''X''的'''维数'''。换句话说，如果 X 最少需要''n''个向量来张出它，那么''X''就是''n''维的。
		+
		+	直观地，一个图形的维数可以认为是一个人要想达到这个图形中所有的点，需要运动的所有不同方向的数目。
		+
		+	例如，一个点是一个零维图形。我们不需要任何向量来张出它，因为如果我们从这个点出发，我们已经到达了它所有的位置。
		+
		+	一条直线是一个一维图形。从直线的某一个点上出发，我们需要一个指向这个直线的方向的向量来到达到直线上的其他点。只要一个向量就足够了，因为通过不同程度的伸缩它我们可以到达直线上的任意其他点。
		+
		+	一个平面是一个二维图形。给定平面上的一个起始点，我们至少需要两个互不平行的向量来张出这个平面。如果只有一个向量，我们只能到达某一条直线上的所有点；所以我们需要有另一个与它不平行的向量来往这条直线的“两边”走，从而到达平面上的其他点。只要两个方向就足够了，因为我们可以顺着（或逆着）前一个向量走不同的距离，再往两边走不同的距离来到达平面上的任意点。也可以把平面理解成许多平行线的“堆积”；要想在二维平面上从一点运动到另一点，我们需要首先沿着线平行线运动，再穿过这些平行线向另一个方向运动。
		+
		+	在我们的眼中，[[欧几里得空间|空间]]是三维的。要达到空间中的某一点，我们不仅要向前向后、向两边走，还需要上下移动。换句话说，需要第三个向量才能到达空间中的所有点。同样，也可以把空间理解成许多平行平面的堆积：要想在空间中从一点运动到另一点，我们可以先沿着一个方向前后走，再向两边走，最后上下走。
		+
		+	四维空间则是一个需要四个不同方向才能到达其中所有点的空间。这种空间可以认为是许多平行的三维空间的堆积。要理解这个概念，想象一下把一张张纸并列叠起来的过程。如果人不把它们一个个堆叠起来，这些纸张不会延伸进三维空间。以同样的方式，要想进入四维空间，就必须向一个新的方向运动，这个方向必须是在三维空间以外的。要达到四维空间中的每一个点，一个人不仅需要向前后、左右、上下移动，还要沿着一对新的方向运动，即上文提到的安娜/卡塔，或者叫维因/维奥等等。
		+
		+	=== 维数 类 比 ===
		+
		+	[[File:Tesseract net.svg|thumb|一个[[超正方体]]的展开图。
		+
		+	要理解四维空间的本性，我们可以通过与低维度类比进行推广。维数类比是指通过研究''n'' - 1维与''n''维之间的关系，来推断''n''维与''n'' + 1维之间会有什么样的关系。<ref>Michio Kaku (1994). ''Hyperspace (book)|Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the Tenth Dimension'', Part&nbsp;I, chapter&nbsp;3, ''The Man Who "Saw" the Fourth Dimension (about tesseracts in years 1870 - 1910)''. ISBN 0-19-286189-1.</ref>
		+
		+	埃德温·阿伯特·阿伯特在他的书平面国 中 运用维数类比，讲述了在一个扁平得就像一张纸的二维世界中生活的一个正方形的故事。<ref>[http://books.google.com/books?id=zRnUHEAAPEAC Google Books] ''Flatland: A Romance of Many Dimensions''. By Edwin A. Abbott, Published by Filiquarian Publishing, LLC., 2007. ISBN 1-59986-928-4, 9781599869285, 148 pages</ref>在这个正方形的眼中，生活在三维世界中的人们拥有近乎神的力量，因为他们能在不打破（二维的）保险箱的情况下从其中把东西（通过移入移出三维空间的方法）取出，能看到所有在二维世界看来是被挡在墙后面的东西，甚至能站在离二维世界几英寸的地方来保持“隐形”。
		+
		+	通过应用维数类比，人们可以推断，四维空间中的人在我们三维的视角看来应该有类似的神奇能力。鲁迪·拉克在他的小说《空间世界》（''Spaceland''）中展示了这一点。<ref>[http://books.google.com/books?id=mAeecPTl5N4C Google Books] ''Spaceland: A Novel of the Fourth Dimension''. By Rudy Rucker, Published by Tom Doherty Associates, LLC, 2002. ISBN 0-7653-0366-3, 9780765303660, 304 pages</ref>小说的主人公就遇到了具有神奇能力的四维人。
		+
		+	==== 射影 ====
		+
		+	射影是应用维数类比来想象四维空间的一种有效方法。射影是指用''n'' - 1维空间中的图形来代表''n''维空间中的图形。比如说，电脑屏幕是二维的，而所有三维的人、地方、东西等等的照片都是以射影的形式展现在二维平面上的。这会把三维世界中的深度去除，代之以间接的信息。人眼的[[视网膜]]也是由一层二维的[[感受器]]构成的，但是人脑能够察知三维物体的真实形状；这是根据阴影、[[透视|近大远小]]、双眼视觉等间接信息推断得来的。画家们经常利用透视来赋予二维的图画一种三维（也就是立体）的感觉。
		+
		+	相似地，四维空间中的物体可以以数学的方法射影到三维空间中，从而使观察它们变得更容易。在这种情况下，一个四维的眼的“视网膜”是由一个三维“层”的感受器构成的。假设一个人有这样一只眼，他就可以根据三维图形中的间接信息推断出四维物体的真实形状。
		+
		+	三维物体在人眼视网膜上留下的透视射影会造成近大远小的现象，这样[[大脑]]就可以推断出三维的深度。以同样的方式，四维物体的透视射影会造成相似的“近大远小”的效果。通过应用维数类比，我们可以从这种效果中推断出四维的“深度”。
		+
		+	下面的图片演示了这种规律。我们可以比较一下三维的正方体和类似的四维超正方体的三维射影。-{-|zh:共用;zh-hans:共享;zh-hant:共用;}-
		+
		+	{|class="wikitable" !正方体 !超正方体 !解释 |- |[[File:Cube-face-first.png|160px]] |[[File:Tesseract-perspective-cell-first.png|160px]] | 左边的图片是正对着一个面看到的正方体。四维中超正方体类似的视角是'''正对一个胞看到的透视射影'''，也就是右边的图显示的。就像正方体的投影是一个正方形一样，超正方体的投影是一个正方体。 需要注意的是，正方体的其他5个面在这里是看不见的。它们被看的见的这个面挡住了。相似地，超正方体的其他7个胞也是看不见的，因为它们被看得见的这个胞“挡住”了。但是，这个胞的6个体，却是全见的。而且不是左图中以透视的方式展现的“全见”，而是犹如我们可以普通的全见整个正方形的四条边和内部一样，4维世界的人的眼，是直接全见整个正方体的6个面和内部的。 |- |[[File:Cube-edge-first.png|160px]] |[[File:Tesseract-perspective-face-first.png|160px]] | 左边的图片是正对着一条边看到的正方体。超正方体类似的视角是'''正对一个面看到的透视射影'''（右边的图）。就像正方体正对边的投影是两个梯形一样，超正方体正对面的投影是两个棱台。 在这个视角中，正方体离我们最近的边是红色的面与绿色的面的公共边。同样，超正方体里我们最近的面是红色的胞与绿色的胞的公共面。 |- |[[File:Cube-vertex-first.png|160px]] |[[File:Tesseract-perspective-edge-first.png|160px]] | 左边是一个正对顶点看到的正方体。这与右边超正方体的'''正对一条边看到的透视射影'''相似。就像正方体正对顶点的投影由三个共用一点的梯形组成一样，超正方体正对边的投影由三个共用一边的六面体组成。正方体离我们最近的顶点是三个面的公共点，而超正方体离我们最近的边是投影体中部的三个胞的公共边。 |- |[[File:Cube-edge-first.png|160px]] |[[File:Tesseract-perspective-edge-first.png|160px]] | 我们还可以把正方体的正对边射影和超正方体的正对边射影放在一起，作一个类比。正方体的射影有两个梯形共用一边，而超正方体的射影有'''三'''个六面体共用一边。 |- |[[File:Cube-vertex-first.png|160px]] |[[File:Tesseract-perspective-vertex-first.png|160px]] | 左边是正方体正对点的射影，右边则是超正方体'''正对一个顶点的透视射影'''。正方体的正对点射影有三个围绕一点的四边形，而超正方体的正对点射影有'''四'''个围绕一点的六面体。正方体离我们最近的顶点是位于投影图形中部的三个面的公共点，而超正方体离我们最近的点也是位于投影体中部的，四个胞的公共点。 注意正方体的六个面中，只有三个能被看到，因为其它三个面在正方体的另一边，被这三个面挡住了。相似地，超正方体的八个胞中只有四个能被看到，因为其它四个胞在超正方体的另一边（在四维深度中离我们这一边更远的一边），被看得见的四个胞挡住了。 |}
		+
		+	==== 阴影 ====
		+
		+	一个与射影有密切关系的方法是把四维几何体的阴影在三维空间中显示出来。
		+
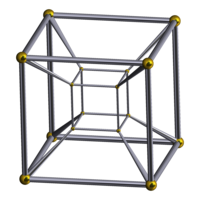
		+	[[File:Schlegel wireframe 8-cell.png|right|200px]] 假设有一束光射向一个三维物体，则其阴影会在二维平面上显示出来。如此类推，光射向二维物体会产生一维阴影，射向一维物体会产生零维阴影，也就是无光的一点；另一方面，光射向四维物体会产生三维阴影。
		+
		+	如果一个立方体的线框置于光源下，其阴影为一正方形位于另一正方形以内，并且相对的点相连。同样，如果[[超正方体|四维正方体]]置于光源下，其阴影便会是一三维正方体位于另一正方体之内，并且相对的点相连。（注意，此处显示的图片乃四维正方体的三维阴影在二维平面上的投影。）
		+
		+	==== 边界 ====
		+
		+	维度类比法也可帮我们推论出高维度物体的基本属性。例如，二维物体有一维的边界，正方形的边界为一维的线；三维物体有二维的边界（表面），正方体的表面为二维的平面。我们可以推论，四维物体便有三维的“边界”，就是超正方体的外围是三维的正方体。以上属性对如何表达四维物体的三维投影很有帮助。
		+
		+	==== [[视觉]]观测 ====
		+
		+	作为三维空间中的生物，我们的眼睛只能看到这个世界的二维投影。生活在四维空间的生物便能看到它们的世界的三维投影。例如，它们可以同时看到一个正方体的所有六面，还能同时看到正方体中的物体；其实我们也可以同时看到二维平面上的正方形的全部四条边及其中的物体。四维生物能同一时间看到三维空间中的所有点、物体和物体的内部，这些是我们在三维空间中看不到的。
		+
		+	==== 限制 ====
		+
		+	类比法是理解高维度空间的一项很好的方法，但我们若不经过更进一步的计算仍不可以妄下结论。以下是圆形周长公式： <math>C = 2\pi r</math> 及球体表面积公式： <math>A = 4\pi r^2</math>。 有人可能会立即推论出超[[球体]]的表面体积为<math>V=6\pi r^3</math>或<math>V=8\pi r^3</math>，但实际上两者均为错误。正确公式为<math>V = 2\pi^2 r^3</math>。
		+
		+	== 几何 ==
		+
		+	四维几何比三维几何丰富得多，因为其额外的维度提供了更多的自由空间。
		+
		+	三维空间中，我们可以从多边形做出多面体；同样地，在四维空间中我们可以从多面体做出多[[胞体]]（四维多胞形）。三维空间中存在5种正多面体，以柏拉图立体称之；而四维空间中存在6种正多胞体，均从柏拉图立体类比而成。三维空间中存在13种半正多面体（阿基米德立体），而在四维空间中存在58种半正多胞体。
		+
		+	在三维空间，我们可以把圆形向第三维度拉伸形成圆柱体。而在四维空间，我们可以向第四维度拉伸球体形成球柱体（球体为“盖”的柱体），或拉伸圆柱体形成圆柱棱体。我们还可以取两个球体的笛卡尔积得到一个双圆柱体。以上三种均可在四维中“滚动”，但各有不同的属性。
		+
		+	三维中，曲线可以形成结，但曲面并不可以（除非互相交叉穿越）。但在四维中，以曲面形成的结可以经过延伸到第四维度而解开。由于自由度更大，四维中的曲面结比三维中的线结要复杂的多。克莱因瓶便是其中一个例子。另一例子为实射影平面。
		+
		+	=== 超球体 ===
		+
		+	在[[欧几里得空间|四维欧几里得空间]]中与P<sub>0</sub>点有相同距离R的所有点的集合能形成一个超曲面，称为三维球面。此超曲面之包含空间的超体积为：
		+
		+	: <math> \mathbf V = 2 \pi^2 R^3</math>
		+
		+	这是广义相对论中的罗伯逊-沃尔克度规，其中''R''由''R(t)''代替，''t''代表宇宙年龄。''R''值的随时间的加大或减低表示宇宙[[膨胀]]或收缩，这取决于宇宙质量密度。<ref>Ray d'Inverno (1992), ''Introducing Einstein's Relativity'', Clarendon Press, chp. 22.8 ''Geometry of 3-spaces of constant curvature'', p.319ff, ISBN 0-19-859653-7</ref>
		+
		+	== 参见 ==
		+
		+	<div style="-moz-column-count:2; column-count:2;">
		+	* [[欧几里得空间]]
		+	* [[欧几里得几何]]
		+	* [[维度]]
		+	* [[五维]]
		+	* [[多胞形]]
		+	* [[三维曲面]]
		+
		+	</div>
		+
		+	== 参考文献 ==
		+
		+	{{Reflist}}
		+
		+	== 外部链接 ==
		+	* [http://www.dimensions-math.org/ Dimensions维度]
		+
		+	{{维度}}
		+
		+	[[Category:相对论|S]]
		+
		+	[[Category:维度|S]] [[Category:四维几何| ]]
		+	==参考来源==
		+	*[http://zh.wikipedia.org/wiki/%E5%9B%9B%E7%BB%B4%E7%A9%BA%E9%97%B4 维基百科-四维空间]

---

在2014年10月4日 (六) 23:14所做的修訂版本

A+醫學百科 >> 四維

Template:Redirect2 [[File:8-cell-simple.gif|thumb|200px|從三維投影看，一個在四維空間中繞一個平面旋轉的四維超正方體。

在物理學和數學中，一個n個數的序列可以被理解為一個n維空間中的位置。當n=4時，所有這樣的位置的集合就叫做四維空間。這種空間與我們熟悉並在其中居住的三維空間不同，因為它多一個維數。這個額外的維數既可以理解成時間，也可以直接理解為空間的第四維，即第四空間維數。

目錄 1 作為時間的第四維數 2 作為空間的第四維數 2.1 正交性 2.2 向量 2.2.1 向量運算 2.2.2 向量操作 2.2.3 向量組合 2.2.4 向量基底 2.2.5 維數 2.3 維數類比 2.3.1 射影 2.3.2 陰影 2.3.3 邊界 2.3.4 視覺觀測 2.3.5 限制 3 幾何 3.1 超球體 4 參見 5 參考文獻 6 外部連結 7 參考來源

作為時間的第四維數

主條目：時空

當人們說到「四維空間」時，經常指的都是關於時間的概念。在這種情況下，四維空間可以理解為三維空間附加一條時間軸。這種空間叫做閔可夫斯基時空或「(3 + 1)-空間」^[1]。這也是愛因斯坦在他的廣義相對論和狹義相對論中提及的四維時空概念。

作為空間的第四維數

第四維數可以用空間的方式理解，即一個有四個空間性維數的空間（「純空間性」的四維空間），或者說有四個兩兩正交的運動方向的空間。這種空間就是數學家們用來研究四維幾何物體的空間，與愛因斯坦提出的時間作為第四維數的理論不同。關於這一點，考克斯特曾寫道：

把時間作為第四維數帶來的好處即使有的話也是微不足道的。實際上，H. G. 威爾在《時間機器》中發展的這種十分吸引人的觀點導致了J. W. 杜恩（《時間實驗》）等作者對相對論的非常錯誤的理解。閔可夫斯基的時空幾何是不符合歐幾里得體系的，所以也就與當前的研究沒有關係。- H. S. M. 考克斯特, Regular Polytopes^[2]

從數學方面講，普通三維空間集合的四維等價物是歐幾里得四維空間，一個四維歐幾里得賦范向量空間。一個向量的「長度」

以標準基底表示就是

也就是勾股定理向四維空間進行的很自然的類比。這就讓兩個向量之間的夾角很容易定義了（參見歐幾里得空間）。

正交性

在我們熟悉的三維空間里，有三對主要方向：上下（高度），南北（緯度），東西（經度）。這三對方向兩兩正交，也就是說，它們兩兩成直角。從數學方面講，它們在三條不同的坐標軸x、y、z上。計算機圖形學中講的深度緩衝指的就是這條z軸，在計算機的二維螢幕上代表深度。

純空間性的四維空間另有一對垂直於其他三個主要方向的主要方向。這一對方向處在另一條同時垂直於x、y、z軸的坐標軸上，通常稱作w軸。對這兩個方向的命名，人們的看法不一。一些現行的命名有安娜/卡塔，斯皮希圖/斯帕提圖，維因/維奧，和宇普西龍/德爾塔。這些額外的方向處於（實際上是垂直於）我們所能觀察到的三維世界中的方向之外。

向量

Template:Expert

主條目：向量

純空間性四維空間可以以向量的形式理解。一個四維向量同樣由方向和長度（又叫做模）組成，它可以認為是對從一個點到另一個點向某個方向移動一定的長度的這個過程的描述。零向量是一個長度為零的特殊向量，也就是描述「不移動」這個過程的向量。

向量運算

數學上四維空間可以簡單理解為有四個坐標軸的空間，即在普通坐標系中需要4個參數來描述其中一點的坐標。 假設一個描述四維空間中一個點的向量為a，有

上式也可以寫成由4個基底(如e₁, e₂, e₃, e₄)表示的形式，則

所以a可化為

四維向量的加法，減法和向量比例和空間向量的一致。空間向量中的數量積（或稱為向量的「內積」、點乘）也被推廣到四維向量中，如

下式可以用於計算一個四維向量的長度

而兩個向量的夾角可由下式定義或計算

向量積（或稱為向量的「外積」、叉乘）是一個常數，而空間向量的外代數定義為

這是雙矢量的求值，以基底(e₁₂, e₁₃, e₁₄, e₂₃, e₂₄, e₃₄)在四維空間中的雙矢構成了六維線性空間，它們可以被用來在四個方向產生旋轉。

向量操作

通過改變一個四維向量的長度而不改變它的方向，我們可以對一個向量進行伸縮變換|伸縮。這可以被想像成沿著原向量的方向伸長或縮短一段長度。一個長度為負數的向量與和它方向相反、長度相等的正數的向量互為相反向量。這可以想像成面沿著原向量的方向倒著走。

如果沿著兩個首尾相接的向量運動，那麼描述這種運動的直接結果的向量就叫做這兩個向量的向量和。例如，如果一個人從點A開始沿某一向量運動到點B，又從點B開始沿另一個向量運動到點C，那麼這兩個向量的和向量就是從點A徑直到點C的向量。

向量組合

主條目：線性組合

給定一組四維向量，我們可以對它們進行任意的伸縮和求和操作來得到新的四維向量。以這種方式得到的所有的四維向量的集合就叫做這一組向量的組合。這種組合可以認為是一個點通過沿著一組向量中的某些向量移動所能達到的所有位置的集合。

給定幾何圖形X和向量集合S，如果從幾何圖形X內的一個點出發，沿著向量集合S的線性組合中的向量運動，能夠到達X內所有其它的點，那麼我們就說這個向量集合S可以張出幾何圖形X。

向量基底

主條目：基底

能夠張出一個幾何圖形X的最小向量集合叫做X的一組基底。不是所有的向量集合都是基底，因為它們可能含有贅余的向量。如果一個向量能通過集合中其他向量經過伸縮、求和而得到，那麼這個向量就是贅余的。例如，如果一個集合中有兩個平行的向量，那麼它們中的一個可以被移除而 X 中的所有點仍然可以達到，因為能通過那個被移除的向量達到的點一定可以通過那個與它平行的向量達到。或者，如果一個向量是其他兩個的和，那麼它也完全可以被移除。零向量總是贅余的，因為它並不能讓一個人達到任意一個除他已經能夠達到的點之外的點。

維數

通過把任意一個可以張出幾何圖形X的向量集合中的所有贅余向量移除，我們可以過的一組X的基底。選定的初始向量集合不同，獲得的能張出 X 的基底也可能不同；但是，可以證明所有這些基底中都含有相同數量的向量。這個數量就叫做X的維數。換句話說，如果 X 最少需要n個向量來張出它，那麼X就是n維的。

直觀地，一個圖形的維數可以認為是一個人要想達到這個圖形中所有的點，需要運動的所有不同方向的數目。

例如，一個點是一個零維圖形。我們不需要任何向量來張出它，因為如果我們從這個點出發，我們已經到達了它所有的位置。

一條直線是一個一維圖形。從直線的某一個點上出發，我們需要一個指向這個直線的方向的向量來到達到直線上的其他點。只要一個向量就足夠了，因為通過不同程度的伸縮它我們可以到達直線上的任意其他點。

一個平面是一個二維圖形。給定平面上的一個起始點，我們至少需要兩個互不平行的向量來張出這個平面。如果只有一個向量，我們只能到達某一條直線上的所有點；所以我們需要有另一個與它不平行的向量來往這條直線的「兩邊」走，從而到達平面上的其他點。只要兩個方向就足夠了，因為我們可以順著（或逆著）前一個向量走不同的距離，再往兩邊走不同的距離來到達平面上的任意點。也可以把平面理解成許多平行線的「堆積」；要想在二維平面上從一點運動到另一點，我們需要首先沿著線平行線運動，再穿過這些平行線向另一個方向運動。

在我們的眼中，空間是三維的。要達到空間中的某一點，我們不僅要向前向後、向兩邊走，還需要上下移動。換句話說，需要第三個向量才能到達空間中的所有點。同樣，也可以把空間理解成許多平行平面的堆積：要想在空間中從一點運動到另一點，我們可以先沿著一個方向前後走，再向兩邊走，最後上下走。

四維空間則是一個需要四個不同方向才能到達其中所有點的空間。這種空間可以認為是許多平行的三維空間的堆積。要理解這個概念，想像一下把一張張紙並列疊起來的過程。如果人不把它們一個個堆疊起來，這些紙張不會延伸進三維空間。以同樣的方式，要想進入四維空間，就必須向一個新的方向運動，這個方向必須是在三維空間以外的。要達到四維空間中的每一個點，一個人不僅需要向前後、左右、上下移動，還要沿著一對新的方向運動，即上文提到的安娜/卡塔，或者叫維因/維奧等等。

維數類比

[[File:Tesseract net.svg|thumb|一個超正方體的展開圖。

要理解四維空間的本性，我們可以通過與低維度類比進行推廣。維數類比是指通過研究n - 1維與n維之間的關係，來推斷n維與n + 1維之間會有什麼樣的關係。^[3]

埃德溫·阿伯特·阿伯特在他的書平面國中運用維數類比，講述了在一個扁平得就像一張紙的二維世界中生活的一個正方形的故事。^[4]在這個正方形的眼中，生活在三維世界中的人們擁有近乎神的力量，因為他們能在不打破（二維的）保險箱的情況下從其中把東西（通過移入移出三維空間的方法）取出，能看到所有在二維世界看來是被擋在牆後面的東西，甚至能站在離二維世界幾英寸的地方來保持「隱形」。

通過應用維數類比，人們可以推斷，四維空間中的人在我們三維的視角看來應該有類似的神奇能力。魯迪·拉克在他的小說《空間世界》（Spaceland）中展示了這一點。^[5]小說的主人公就遇到了具有神奇能力的四維人。

射影

射影是應用維數類比來想像四維空間的一種有效方法。射影是指用n - 1維空間中的圖形來代表n維空間中的圖形。比如說，電腦螢幕是二維的，而所有三維的人、地方、東西等等的照片都是以射影的形式展現在二維平面上的。這會把三維世界中的深度去除，代之以間接的信息。人眼的視網膜也是由一層二維的感受器構成的，但是人腦能夠察知三維物體的真實形狀；這是根據陰影、近大遠小、雙眼視覺等間接信息推斷得來的。畫家們經常利用透視來賦予二維的圖畫一種三維（也就是立體）的感覺。

相似地，四維空間中的物體可以以數學的方法射影到三維空間中，從而使觀察它們變得更容易。在這種情況下，一個四維的眼的「視網膜」是由一個三維「層」的感受器構成的。假設一個人有這樣一隻眼，他就可以根據三維圖形中的間接信息推斷出四維物體的真實形狀。

三維物體在人眼視網膜上留下的透視射影會造成近大遠小的現象，這樣大腦就可以推斷出三維的深度。以同樣的方式，四維物體的透視射影會造成相似的「近大遠小」的效果。通過應用維數類比，我們可以從這種效果中推斷出四維的「深度」。

下面的圖片演示了這種規律。我們可以比較一下三維的正方體和類似的四維超正方體的三維射影。

陰影

一個與射影有密切關係的方法是把四維幾何體的陰影在三維空間中顯示出來。

假設有一束光射向一個三維物體，則其陰影會在二維平面上顯示出來。如此類推，光射向二維物體會產生一維陰影，射向一維物體會產生零維陰影，也就是無光的一點；另一方面，光射向四維物體會產生三維陰影。

如果一個立方體的線框置於光源下，其陰影為一正方形位於另一正方形以內，並且相對的點相連。同樣，如果四維正方體置於光源下，其陰影便會是一三維正方體位於另一正方體之內，並且相對的點相連。（注意，此處顯示的圖片乃四維正方體的三維陰影在二維平面上的投影。）

邊界

維度類比法也可幫我們推論出高維度物體的基本屬性。例如，二維物體有一維的邊界，正方形的邊界為一維的線；三維物體有二維的邊界（表面），正方體的表面為二維的平面。我們可以推論，四維物體便有三維的「邊界」，就是超正方體的外圍是三維的正方體。以上屬性對如何表達四維物體的三維投影很有幫助。

視覺觀測

作為三維空間中的生物，我們的眼睛只能看到這個世界的二維投影。生活在四維空間的生物便能看到它們的世界的三維投影。例如，它們可以同時看到一個正方體的所有六面，還能同時看到正方體中的物體；其實我們也可以同時看到二維平面上的正方形的全部四條邊及其中的物體。四維生物能同一時間看到三維空間中的所有點、物體和物體的內部，這些是我們在三維空間中看不到的。

限制

類比法是理解高維度空間的一項很好的方法，但我們若不經過更進一步的計算仍不可以妄下結論。以下是圓形周長公式： C = 2πr 及球體表面積公式： A = 4πr²。 有人可能會立即推論出超球體的表面體積為V = 6πr³或V = 8πr³，但實際上兩者均為錯誤。正確公式為V = 2π²r³。

幾何

四維幾何比三維幾何豐富得多，因為其額外的維度提供了更多的自由空間。

三維空間中，我們可以從多邊形做出多面體；同樣地，在四維空間中我們可以從多面體做出多胞體（四維多胞形）。三維空間中存在5種正多面體，以柏拉圖立體稱之；而四維空間中存在6種正多胞體，均從柏拉圖立體類比而成。三維空間中存在13種半正多面體（阿基米德立體），而在四維空間中存在58種半正多胞體。

在三維空間，我們可以把圓形向第三維度拉伸形成圓柱體。而在四維空間，我們可以向第四維度拉伸球體形成球柱體（球體為「蓋」的柱體），或拉伸圓柱體形成圓柱稜體。我們還可以取兩個球體的笛卡爾積得到一個雙圓柱體。以上三種均可在四維中「滾動」，但各有不同的屬性。

三維中，曲線可以形成結，但曲面並不可以（除非互相交叉穿越）。但在四維中，以曲面形成的結可以經過延伸到第四維度而解開。由於自由度更大，四維中的曲面結比三維中的線結要複雜的多。克萊因瓶便是其中一個例子。另一例子為實射影平面。

超球體

在四維歐幾里得空間中與P₀點有相同距離R的所有點的集合能形成一個超曲面，稱為三維球面。此超曲面之包含空間的超體積為：

這是廣義相對論中的羅伯遜-沃爾克度規，其中R由R(t)代替，t代表宇宙年齡。R值的隨時間的加大或減低表示宇宙膨脹或收縮，這取決於宇宙質量密度。^[6]

參見

參考文獻

外部連結

• Dimensions維度

Template:維度

參考來源

• 維基百科-四維空間

關於「四維」的留言：	訂閱討論RSS
目前暫無留言
添加留言

更多醫學百科條目