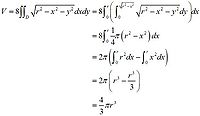球體
| A+醫學百科 >> 球體 |
定義:空間中到定點的距離等於定長的所有點組成的圖形叫做球,如圖右圖所示的圖形為球體。
球面是一個連續曲面的立體圖形,由球面圍成的幾何體稱為球體。
目錄 |
球形的立體物
指球形的體育用品,球類運動,包括手球、籃球、足球、撞球,排球、羽毛球、網球、高爾夫球、冰球、沙灘排球、棒球、壘球、藤球、毽球、桌球、撞球、鞠蹴、板球、壁球、沙壺、冰壺、克郎球、橄欖球、曲棍球、水球、馬球、保齡球、健身球、門球、彈球等。
球體的組成
球的表面是一個曲面,這個曲面就叫做球面。
球和圓類似,也有一個中心叫做球心。
星體,特指「地球」。
數學中的球體
球體基本概念
半圓以它的直徑為旋轉軸,旋轉所成的曲面叫做球面。
球面所圍成的幾何體叫做球體,簡稱球。
半圓的圓心叫做球心。
連結球心和球面上任意一點的線段叫做球的半徑。
連結球面上兩點並且經過球心的線段叫做球的直徑。
球體性質
用一個面去截一個球,截面是圓面。球的截面有以下性質:
1 球心和截面圓心的連線垂直於截面。
2 球心到截面的距離d與球的半徑R及截面的半徑r有下面的關係:r^2=R^2-d^2
球面被經過球心的平面截得的圓叫做大圓,被不經過球心的截面截得的圓叫做小圓。
在球面上,兩點之間的最短連線的長度,就是經過這兩點的大圓在這兩點間的一段劣弧的長度,我們把這個弧長叫做兩點的球面距離。
球體函數
半徑為r的球的函數為:r^2=x^2+y^2+z^2
球體的計算公式
半徑是R的球的體積 計算公式是:V=(4/3)πR^3(三分乘以π乘以半徑的三次)
V=(1/6)πd^3 (六分乘以π乘以直徑的三次)
半徑是R的球的表面積 計算公式是:S=4πR^2(4倍的π乘以R的二次)
證明:
證:V球=4/3*pi*r^3
欲證V球=4/3pi*r^3,可證V半球=2/3pi*r^3
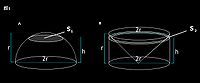
做一個半球h=r, 做一個圓柱h=r(如圖1)
∵V柱-V錐
= pi*r^3- pi*r^3/3
=2/3pi*r^3
∴若猜想成立,則V柱-V錐=V半球
∵根據卡瓦列利原理,夾在兩個平行平面之間的兩個立體圖形,被平行於這兩個平面的任意平面所截,如果所得的兩個截面面積相等,那麼,這兩個立體圖形的體積相等。
∴若猜想成立,兩個平面:S1(圓)=S2(環)
1.從半球高h點截一個面 根據公式可知此面積為pi*(r^2-h^2)^0.5^2=pi*(r^2-h^2)
2.從圓柱做一個與其等底等高的圓錐:V錐 根據公式可知其右側環形的面積為pi*r^2-pi*r*h/r=pi*(r^2-h^2)
∵pi*(r^2-h^2)=pi*(r^2-h^2)
∴V柱-V錐=V半球
∵V柱-V錐=pi*r^3-pi*r^3/3=2/3pi*r^3
∴V半球=2/3pi*r^3
由V半球可推出V球=2*V半球=4/3*pi*r^3
證畢
當然,求球體體積的方法很多,較容易讓人理解的是用重積分的方法
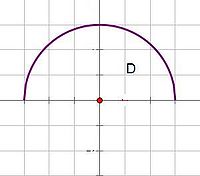
解:積分區域如圖
,圓的半徑為r
| 關於「球體」的留言: | |
|
目前暫無留言 | |
| 添加留言 | |